章末分层突破

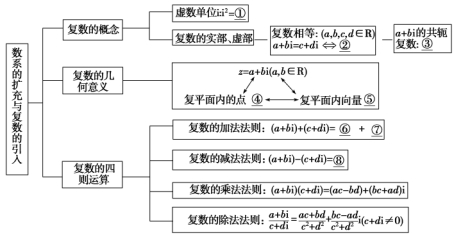
[自我校对]

①－1　②a＝c，b＝d

③z＝a－bi

④Z(a，b)　⑤→(OZ)　⑥a＋c

⑦(b＋d)i

⑧(a－c)＋(b－d)i

　　　　　　　

　　　　　　　

复数的概念

正确确定复数的实、虚部是准确理解复数的有关概念(如实数、虚数、纯虚数、相等复数、共轭复数、复数的模)的前提.

两复数相等的充要条件是复数问题转化为实数问题的依据.

求字母的范围时一定要关注实部与虚部自身有意义.

　复数z＝log₃(x²－3x－3)＋ilog₂(x－3)，当x为何实数时，

(1)z∈R；(2)z为虚数.

【精彩点拨】　根据复数的分类列方程求解.

【规范解答】　(1)因为一个复数是实数的充要条件是虚部为0，

所以x－3>0， ③(log2（x－3）＝0， ②)

由②得x＝4，经验证满足①③式.

所以当x＝4时，z∈R.

(2)因为一个复数是虚数的充要条件是虚部不为0，

所以x－3>0， ③(log2（x－3）≠0， ②)

由①得x>2(21)或x<2(21).

由②得x≠4，由③得x>3.

所以当x>2(21)且x≠4时，z为虚数.

[再练一题]

1.(1)设i是虚数单位，若复数a－3－i(10)(a∈R)是纯虚数，则a的值为(　　)

A.－3 B.－1

C.1 D.3

(2)设复数z满足i(z＋1)＝－3＋2i(i是虚数单位)，则复数z的实部是__________.

【解析】　(1)因为a－3－i(10)＝a－（3－i）（3＋i）(10（3＋i）)＝a－10(10（3＋i）)＝(a－3)－i，由纯虚数的定义，知a－3＝0，所以a＝3.

(2)法一：设z＝a＋bi(a，b∈R)，

则i(z＋1)＝i(a＋bi＋1)＝－b＋(a＋1)i＝－3＋2i.

由复数相等的充要条件，得a＋1＝2，(－b＝－3，)解得b＝3.(a＝1，)

故复数z的实部是1.

法二：由i(z＋1)＝－3＋2i，得z＋1＝i(－3＋2i)＝2＋3i，故z＝1＋3i，即复数z的实部是1.

【答案】　(1)D　(2)1

复数的四则运算

复数加减乘运算可类比多项式的加减乘运算，注意把i看作一个字母(i²＝－1)，除法运算注意应用共轭的性质z·－(z)为实数.

　(1)设i是虚数单位，－(z)表示复数z的共轭复数.若z＝1＋i，则i(z)＋i·－(z)＝(　　)

A.－2 B.－2i

C.2 D.2i

(2)设复数z满足(z－2i)(2－i)＝5，则z＝(　　)

A.2＋3i B.2－3i

C.3＋2i D.3－2i

【精彩点拨】　(1)先求出－(z)及i(z)，结合复数运算法则求解.

(2)利用方程思想求解并化简.

【规范解答】　(1)∵z＝1＋i，∴－(z)＝1－i，i(z)＝i(1＋i)＝i(－i2＋i)＝1－i，∴i(z)＋i·－(z)＝1－i＋i(1－i)＝(1－i)(1＋i)＝2.故选C.

(2)由(z－2i)(2－i)＝5，得z＝2i＋2－i(5)＝2i＋（2－i）（2＋i）(5（2＋i）)＝2i＋2＋i＝2＋3i.

【答案】　(1)C　(2)A

[再练一题]

2.已知(1＋2i) －(z)＝4＋3i，则-()的值为(　　)

A.5(3)＋5(4)i B.5(3)－5(4)i

C.－5(3)＋5(4)i D.－5(3)－5(4)i

【解析】　因为(1＋2i) －(z)＝4＋3i，所以－(z)＝1＋2i(4＋3i)＝5(（4＋3i）（1－2i）)＝2－i，所以z＝2＋i，所以-()＝2－i(2＋i)＝5(（2＋i）2)＝5(3)＋5(4)i.

【答案】　A

复数的几何意义

1.复数的几何表示法：即复数z＝a＋bi(a，b∈R)可以用复平面内的点Z(a，b)来表示.此类问题可建立复数的实部与虚部应满足的条件，通过解方程(组)或不等式(组)求解.

2.复数的向量表示：以原点为起点的向量表示的复数等于它的终点对应的复数；向量平移后，此向量表示的复数不变，但平移前后起点、终点对应的复数要改变.

　(1)在复平面内，复数1＋i(i)对应的点位于(　　)

A.第一象限 B.第二象限

C.第三象限 D.第四象限

(2)在复平面内，复数2＋i(1－2i)对应的点的坐标为(　　)

A.(0，－1) B.(0，1)

C.5(3) D.5(3)

【精彩点拨】　先把复数z化为复数的标准形式，再写出其对应坐标.

【规范解答】　(1)复数1＋i(i)＝（1＋i）（1－i）(i（1－i）)＝2(1＋i)＝2(1)＋2(1)i.

∴复数对应点的坐标是2(1).

∴复数1＋i(i)在复平面内对应的点位于第一象限.故选A.

(2)∵2＋i(1－2i)＝（2＋i）（2－i）(（1－2i）（2－i）)＝5(－5i)＝－i，其对应的点为(0，－1)，故选A.

【答案】　(1)A　(2)A

[再练一题]

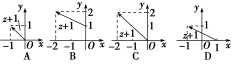
3.(1)已知复数z对应的向量如图5­1所示，则复数z＋1所对应的向量正确的是(　　)

图5­1

(2)若i为虚数单位，图5­2中复平面内点Z表示复数z，则表示复数1＋i(z)的点是(　　)

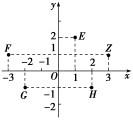
图5­2

A.E  B.F　　　C.G　　　D.H

【解析】　(1)由题图知，z＝－2＋i，∴z＋1＝－2＋i＋1＝－1＋i，故z＋1对应的向量应为选项A.

(2)由题图可得z＝3＋i，所以1＋i(z)＝1＋i(3＋i)＝（1＋i）（1－i）(（3＋i）（1－i）)＝2(4－2i)＝2－i，则其在复平面上对应的点为H(2，－1).

【答案】　(1)A　(2)D

转化与化归思想

一般设出复数z的代数形式，即z＝x＋yi(x，y∈R)，则涉及复数的分类、几何意义、模的运算、四则运算、共轭复数等问题，都可以转化为实数x，y应满足的条件，即复数问题实数化的思想是本章的主要思想方法.

　设z∈C，满足z＋z(1)∈R，且z－4(1)是纯虚数，求z.

【精彩点拨】　本题关键是设出z代入题中条件进而求出z.

【规范解答】　设z＝x＋yi(x，y∈R)，则

z＋z(1)＝x＋yi＋x＋yi(1)

＝x2＋y2(x)＋x2＋y2(y)i，

∵z＋z(1)∈R，

∴y－x2＋y2(y)＝0，

解得y＝0或x²＋y²＝1，

又∵z－4(1)＝x＋yi－4(1)＝4(1)＋yi是纯虚数.

∴y≠0，(＝0，)

∴x＝4(1)，代入x²＋y²＝1中，求出y＝±4(15)，

∴复数z＝4(1)±4(15)i.

[再练一题]

4.满足z＋z(5)是实数，且z＋3的实部与虚部是相反数的虚数z是否存在？若存在，求出虚数z；若不存在，请说明理由.

【解】　设虚数z＝x＋yi(x，y∈R，且y≠0)，

则z＋z(5)＝x＋yi＋x＋yi(5)＝x＋x2＋y2(5x)＋x2＋y2(5y)i，z＋3＝x＋3＋yi.

由已知，得x＋3＝－y，(＝0，)

因为y≠0，

所以x＋y＝－3，(x2＋y2＝5，)解得y＝－2(x＝－1，)或y＝－1.(x＝－2，)

所以存在虚数z＝－1－2i或z＝－2－i满足题设条件.

1.(2016·全国卷Ⅱ)设复数z满足z＋i＝3－i，则－(z)＝(　　)

A.－1＋2i B.1－2i

C.3＋2i D.3－2i

【解析】　由z＋i＝3－i得z＝3－2i，∴－(z)＝3＋2i，故选C.

【答案】　C

2.(2015·广东高考)若复数z＝i(3－2i)(i是虚数单位)，则－(z)＝(　　)

A.2－3i B.2＋3i

C.3＋2i D.3－2i

【解析】　∵z＝i(3－2i)＝3i－2i²＝2＋3i，∴－(z)＝2－3i.

【答案】　A

3.(2015·安徽高考)设i是虚数单位，则复数1－i(2i)在复平面内所对应的点位于(　　)

A.第一象限 B.第二象限

C.第三象限 D.第四象限

【解析】　1－i(2i)＝（1－i）（1＋i）(2i（1＋i）)＝2(2（i－1）)＝－1＋i，由复数的几何意义知－1＋i在复平面内的对应点为(－1，1)，该点位于第二象限，故选B.

【答案】　B

4.(2015·山东高考)若复数z满足z()＝i，其中i为虚数单位，则z＝(　　)

A.1－i B.1＋i

C.－1－i D.－1＋i

【解析】　由已知得－(z)＝i(1－i)＝i＋1，则z＝1－i，故选A.

【答案】　A

5.(2016·全国卷Ⅰ)设(1＋2i)(a＋i)的实部与虚部相等，其中a为实数，则a＝(　　)

A.－3 B.－2

C.2 D.3

【解析】　(1＋2i)(a＋i)＝a－2＋(1＋2a)i，由题意知a－2＝1＋2a，解得a＝－3，故选A.

【答案】　A

章末综合测评(五)　数系的扩充与复数的引入

(时间120分钟，满分150分)

一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的)

1.已知a，b∈C，下列命题正确的是(　　)

A.3i<5i　 B.a＝0⇔|a|＝0

C.若|a|＝|b|，则a＝±b D.a²≥0

【解析】　A选项中，虚数不能比较大小；B选项正确；C选项中，当a，b∈R时，结论成立，但在复数集中不一定成立，如|i|＝3()，但i≠－2(1)＋2(3)i或2(1)－2(3)i；D选项中，当a∈R时结论成立，但在复数集中不一定成立，如i²＝－1<0.

【答案】　B

2.i是虚数单位，则1＋i(i)的虚部是(　　)

A.2(1)i　 B.－2(1)i

C.2(1) D.－2(1)

【解析】　1＋i(i)＝（1＋i）（1－i）(i（1－i）)＝2(1＋i)＝2(1)＋2(1)i.

【答案】　C

3.1＋i(2)＝(　　)

A.2 B.2

C. D.1

【解析】　由1＋i(2)＝（1＋i）（1－i）(2（1－i）)＝2(2－2i)＝1－i，

∴1＋i(2)＝|1－i|＝.故选C.

【答案】　C

4. -(z)是z的共轭复数.若z＋-(z)＝2，(z－-(z))i＝2(i为虚数单位)，则z＝(　　)

A.1＋i B.－1－i

C.－1＋i D.1－i

【解析】　法一：设z＝a＋bi，a，b为实数，则－(z)＝a－bi，∵z＋－(z)＝2a＝2，∴a＝1.又(z－－(z))i＝2bi²＝－2b＝2，∴b＝－1.故z＝1－i.

法二：∵(z－－(z))i＝2，∴z－－(z)＝i(2)＝－2i.又z＋－(z)＝2，∴(z－－(z))＋(z＋－(z))＝－2i＋2，∴2z＝－2i＋2，

∴z＝1－i.

【答案】　D

5.复数1－i(i)的共轭复数为(　　)

【导学号：94210087】

A.－2(1)＋2(1)i B.2(1)＋2(1)i

C.2(1)－2(1)i D.－2(1)－2(1)i

【解析】　∵1－i(i)＝（1－i）（1＋i）(i（1＋i）)＝2(－1＋i)＝－2(1)＋2(1)i，

∴其共轭复数为－2(1)－2(1)i.故选D.

【答案】　D

6.下面是关于复数z＝－1＋i(2)的四个命题：

p₁：|z|＝2；

p₂：z²＝2i；

p₃：z的共轭复数为1＋i；

p₄：z的虚部为－1.

其中的真命题为(　　)

A.p₂，p₃ B.p₁，p₂

C.p₂，p₄ D.p₃，p₄

【解析】　∵z＝－1＋i(2)＝－1－i，

∴|z|＝＝，

∴p₁是假命题；

∵z²＝(－1－i)²＝2i，∴p₂是真命题；

∵z＝－1＋i，∴p₃是假命题；

∵z的虚部为－1，∴p₄是真命题.

其中的真命题为p₂，p₄.

【答案】　C

7.复平面上平行四边形ABCD的四个顶点中，A，B，C所对应的复数分别为2＋3i，3＋2i，－2－3i，则D点对应的复数是(　　)

A.－2＋3i B.－3－2i

C.2－3i D.3－2i

【解析】　设D(x，y)，由平行四边形对角线互相平分得，(2＋y)∴y＝－2，(x＝－3，)

∴D(－3，－2)，∴对应复数为－3－2i.

【答案】　B

8.若复数(a²－a－2)＋(|a－1|－1)i(a∈R)不是纯虚数，则(　　)

A.a＝－1 B.a≠－1且a≠2

C.a≠－1 D.a≠2

【解析】　要使复数不是纯虚数，则有

|a－1|－1≠0，(a2－a－2≠0，)

解得a≠－1.

【答案】　C

9.若a，b∈R，则复数(a²－6a＋10)＋(－b²＋4b－5)i对应的点在(　　)

A.第一象限 B.第二象限

C.第三象限 D.第四象限

【解析】　复数对应点的坐标为(a²－6a＋10，－b²＋4b－5)，

又∵a²－6a＋10＝(a－3)²＋1>0，

－b²＋4b－5＝－(b－2)²－1<0.

∴复数对应的点在第四象限.故选D.

【答案】　D

10.如果复数z＝3＋ai满足条件|z－2|<2，那么实数a的取值范围是(　　)

A.(－2，2) B.(－2，2)

C.(－1，1) D.(－， )

【解析】　因为|z－2|＝|3＋ai－2|＝|1＋ai|＝<2，所以a²＋1<4，所以a²<3，即－<a<.

【答案】　D

11.若1＋i是关于x的实系数方程x²＋bx＋c＝0的一个复数根，则(　　)

A.b＝2，c＝3 B.b＝－2，c＝3

C.b＝－2，c＝－1 D.b＝2，c＝－1

【解析】　因为1＋i是实系数方程的一个复数根，所以1－i也是方程的根，则1＋i＋1－i＝2＝－b，(1＋i)(1－i)＝3＝c，解得b＝－2，c＝3.

【答案】　B

12.设z是复数，则下列命题中的假命题是(　　)

A.若z²≥0，则z是实数

B.若z²<0，则z是虚数

C.若z是虚数，则z²≥0

D.若z是纯虚数，则z²<0

【解析】　设z＝a＋bi(a，b∈R)，

选项A，z²＝(a＋bi)²＝a²－b²＋2abi≥0，则a2≥b2，(ab＝0，)故b＝0或a，b都为0，即z为实数，正确.

选项B，z²＝(a＋bi)²＝a²－b²＋2abi<0，则a2<b2，(ab＝0，)则b≠0，(a＝0，)故z一定为虚数，正确.

选项C，若z为虚数，则b≠0，z²＝(a＋bi)²＝a²－b²＋2abi，

由于a的值不确定，故z²无法与0比较大小，错误.

选项D，若z为纯虚数，则b≠0，(a＝0，)则z²＝－b²<0，正确.

【答案】　C

二、填空题(本大题共4小题，每小题5分，共20分.将答案填在题中的横线上)

13.(2015·重庆高考)设复数a＋bi(a，b∈R)的模为，则(a＋bi)(a－bi)＝________.

【解析】　∵|a＋bi|＝＝，∴(a＋bi)(a－bi)＝a²＋b²＝3.

【答案】　3

14.a为正实数，i为虚数单位，i(a＋i)＝2，则a＝__________.

【解析】　i(a＋i)＝i·（－i）(（a＋i）·（－i）)＝1－ai，

则i(a＋i)＝|1－ai|＝＝2，所以a²＝3.

又a为正实数，所以a＝.

【答案】　

15.设a，b∈R，a＋bi＝1－2i(11－7i)(i为虚数单位)，则a＋b的值为__________.

【导学号：94210088】

【解析】　a＋bi＝1－2i(11－7i)＝（1－2i）（1＋2i）(（11－7i）（1＋2i）)＝5(25＋15i)＝5＋3i，依据复数相等的充要条件可得a＝5，b＝3.

从而a＋b＝8.

【答案】　8

16.若复数z满足|z－i|≤(i为虚数单位)，则z在复平面内所对应的图形的面积为________.

【解析】　设z＝x＋yi(x，y∈R)，则由|z－i|≤可得≤，即x²＋(y－1)²≤2，它表示以点(0，1)为圆心，为半径的圆及其内部，所以z在复平面内所对应的图形的面积为2π.

【答案】　2π

三、解答题(本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤)

17.(本小题满分10分)计算：

(1)(＋i)²(4＋5i)；

(2)（1－i）2(2＋2i)＋1＋i(2).

【解】　(1)(＋i)²(4＋5i)＝2(1＋i)²(4＋5i)

＝4i(4＋5i)＝－20＋16i.

(2)（1－i）2(2＋2i)＋1＋i(2)

＝－2i(2＋2i)＋2i(2)

＝i(1＋i)＋i(1)

＝－1＋i＋(－i)^{1 008}

＝－1＋i＋1

＝i.

18.(本小题满分12分)已知关于x，y的方程组（2x＋ay）－（4x－y＋b）i＝9－8i，②(（2x－1）＋i＝y－（3－y）i，①)有实数解，求实数a，b的值.

【解】　由①得y－3＝1，(2x－1＝y，)解得y＝4，(，)

将x，y代入②得(5＋4a)－(6＋b)i＝9－8i，

所以－（6＋b）＝－8，(5＋4a＝9，)

所以a＝1，b＝2.

19.(本小题满分12分)实数k为何值时，复数z＝(k²－3k－4)＋(k²－5k－6)i是：

(1)实数；(2)虚数；(3)纯虚数；(4)0.

【解】　(1)当k²－5k－6＝0，即k＝6或k＝－1时，z是实数.

(2)当k²－5k－6≠0，即k≠6且k≠－1时，z是虚数.

(3)当k2－5k－6≠0，(k2－3k－4＝0，)即k＝4时，z是纯虚数.

(4)当k2－5k－6＝0，(k2－3k－4＝0，)即k＝－1时，z是0.

20.(本小题满分12分)已知复数z满足|z|＝，z²的虚部是2.

(1)求复数z；

(2)设z，z²，z－z²在复平面上的对应点分别为A，B，C，求△ABC的面积.

【解】　(1)设z＝a＋bi(a，b∈R)，则z²＝a²－b²＋2abi，由题意得a²＋b²＝2且2ab＝2，解得a＝b＝1或a＝b＝－1，所以z＝1＋i或z＝－1－i.

(2)当z＝1＋i时，z²＝2i，z－z²＝1－i，所以A(1，1)，B(0，2)，C(1，－1)，所以S_△ABC＝1.

当z＝－1－i时，z²＝2i，z－z²＝－1－3i，所以A(－1，－1)，B(0，2)，C(－1，－3)，所以S_△ABC＝1.

21.(本小题满分12分)已知复数z₁＝i，z₂＝－i，z₃＝2－i，z₄＝－在复平面上对应的点分别是A，B，C，D.

(1)求证：A，B，C，D四点共圆；

(2)已知→(AB)＝2 →(AP)，求点P对应的复数.

【解】　(1)证明：∵|z₁|＝|z₂|＝|z₃|＝|z₄|＝，

即|OA|＝|OB|＝|OC|＝|OD|，

∴A，B，C，D四点都在圆x²＋y²＝5上，

即A，B，C，D四点共圆.

(2)∵A(0，)，B(，－)，

∴→(AB)＝(，－－).

设P(x，y)，则→(AP)＝(x，y－)，

若→(AB)＝2 →(AP)，那么(，－－)＝(2x，2y－2)，

∴，(2＝2x，)

解得3()

∴点P对应的复数为2(2)＋2(3)i.

22.(本小题满分12分)设O为坐标原点，已知向量→(OZ)₁，→(OZ)₂分别对应复数z₁，z₂，且z₁＝a＋5(3)＋(10－a²)i，z₂＝1－a(2)＋(2a－5)i，a∈R.若－(z1)＋z₂可以与任意实数比较大小，求→(OZ)₁·→(OZ)₂的值.

【解】　由题意，得－(z1)＝a＋5(3)－(10－a²)i，

则－(z1)＋z₂＝a＋5(3)－(10－a²)i＋1－a(2)＋(2a－5)i

＝1－a(2)＋(a²＋2a－15)i.

因为－(z1)＋z₂可以与任意实数比较大小，

所以－(z1)＋z₂是实数，

所以a²＋2a－15＝0，解得a＝－5或a＝3.

又因为a＋5≠0，所以a＝3，所以z₁＝8(3)＋i，z₂＝－1＋i.

所以→(OZ)₁＝，1(3)，→(OZ)₂＝(－1，1).

所以→(OZ)₁·→(OZ)₂＝8(3)×(－1)＋1×1＝8(5).