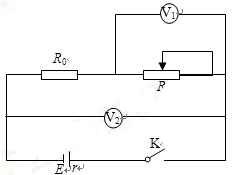
16．目前汽车上都有车载电瓶作为备用电源，用久以后性能会下降，表现之一为电瓶的电动势变小，内阻变大。某兴趣小组将一块旧的车载电瓶充满电，准备利用下列器材测量电瓶的电动势和内电阻。

A．待测电瓶，电动势约为3 V，内阻约几欧姆

B．直流电压表V₁、V₂，量程均为3 V，内阻约为3 kΩ

C．定值电阻R₀未知

D．滑动变阻器R，****阻值R_m

E．导线和开关

（1）根据如图甲所示的实物连接图，在图乙方框中画出相应的电路图。

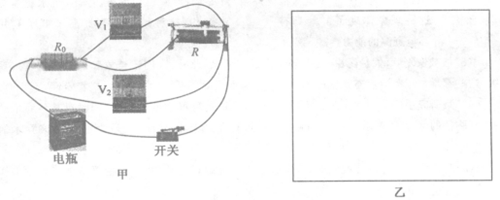
（2）实验之前，需要利用该电路图测出定值电阻R₀，方法是先把滑动变阻器R调到****阻值R_m，再闭合开关，电压表V₁和V₂的读数分别为U₁₀，U₂₀，则R₀＝_________（用U₁₀、U₂₀、R_m表示）

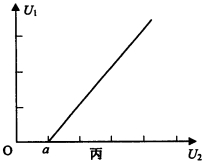
（3）实验中移动滑动变阻器触头，读出电压表V₁和V₂的多组数据U₁、U₂，描绘出U₁一U₂图象如图丙所示，图中直线斜率为k，与横轴的截距为a，则电瓶的电动势E＝________，内阻r＝__________（用k、a、R₀表示）。

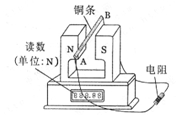17．如图所示为一种可测量磁感应强度的实验装置：磁铁放在水平放置的电子测力计上，两极之间的磁场可视为水平匀强磁场，其余区域磁场的影响可忽略不计，此时电子测力计的示数为G₁。将一直铜条AB水平且垂直于磁场方向静置于磁场中，两端通过导线与一电阻连接成闭合回路，此时电子测力计的示数为G₂。现使铜棒以竖直向下的恒定速率v在磁场中运动，这时电子测力计的示数为G₃，测得铜条在匀强磁场中的长度为L，回路总阻值为R。铜条始终未与磁铁接触。

（1）下列判断正确的是（    ）

A.G₁＜G₂＜G₃       B.G₁＝G₂＜G₃

C.G₁＝G₂＞G₃       D.G₁＜G₂＝G₃

（2）由以上测得量可以写出磁感应强度B大小的表达式为____________。

三、计算题（18题10分，19题12分，20题16分，共38分。解答应写出必要的文字说明、方程式和重要演算步骤，只写出最后答案不能得分；有数值计算的题，答案中必须明确写出数值和单位。)

18（10分）．某地区多发雾霾天气，PM2.5浓度过高，为防控粉尘污染，某同学设计了一种除尘方案，用于清除带电粉尘．模型简化如图所示，粉尘源从A点向水平虚线上方(竖直平面内)各个方向均匀喷出粉尘微粒，每颗粉尘微粒速度大小均为v＝10 m/s，质量为m＝5×10^－10 kg，电荷量为q＝＋1×10^－7 C，粉尘源正上方有一半径R＝0.5 m的圆形边界匀强磁场，磁场的磁感应强度方向垂直纸面向外且大小为B＝0.1 T的，磁场右侧紧靠平行金属极板MN、PQ，两板间电压恒为U₀，两板相距d＝1 m，板长l＝1 m。不计粉尘重力及粉尘之间的相互作用，假设MP为磁场与电场的分界线。（已知，，）求：

（1）微粒在磁场中的半径r并判断粒子出磁场的速度方向；

（2）若粉尘微粒100%被该装置吸收，平行金属极板MN、PQ间电压至少多少？

19（12分）．如图所示，MN、PQ为间距L=0.5 m的足够长平行导轨，NQ⊥MN。导轨平面与水平面间的夹角θ=37°，NQ间连接有一个R=5 Ω 的电阻。有一匀强磁场垂直于导轨平面，磁感应强度为B₀=1 T。将一根质量为m=0.05 kg的金属棒ab紧靠NQ放置在导轨上，且与导轨接触良好，导轨与金属棒的电阻均不计。现由静止释放金属棒，金属棒沿导轨向下运动过程中始终与NQ平行。已知金属棒与导轨间的动摩擦因数μ=0.5，当金属棒滑行至cd处时已经达到稳定速度，cd距离NQ为s=2 m。试解答以下问题：（g=10 m/s²，sin37°=0.6，cos37°=0.8）

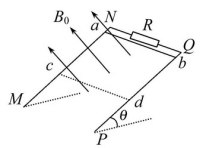
（1）当金属棒滑行至cd处时回路中的电流多大？

（2）金属棒达到的稳定速度是多大？

（3）当金属棒滑行至cd处时回路中产生的焦耳热是多少？

20（16分）．相距L＝1．5 m的足够长金属导轨竖直放置，质量为m₁＝1 kg的金属棒ab和质量为m₂＝0．27 kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上，如图（a）所示，虚线上方磁场方向垂直纸面向里，虚线下方磁场方向竖直向下，两处磁场磁感应强度大小相同。ab棒光滑，cd棒与导轨间动摩擦因数为μ＝0．75，两棒总电阻为1．8Ω，导轨电阻不计。t = 0时刻起，ab棒在方向竖直向上、大小按图（b）所示规律变化的外力F作用下，由静止沿导轨向上匀加速运动，同时也由静止释放cd棒。g取10 m/s²

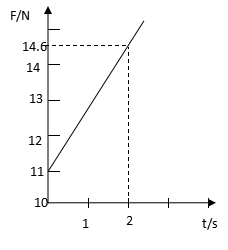
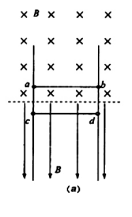
（1）求磁感应强度B的大小和ab棒加速度大小；

（2）已知在2 s内外力F做功40 J，求这一过程中两金属棒产生的总焦耳热；

（3）求出cd棒达到****速度所对应的时刻t₁。

物理试题参考答案

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
C	B	B	B	D	D	D	C	A	D	BC	AB	BD	BD	CD

16【答案】（1）如图所示；

（2）

（3）     

17【答案】（1）B

（2）

18（10分）【答案】(1)0.5m，水平向右  （2）1V  

【解析】

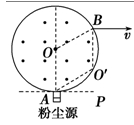
试题分析：(1)粉尘微粒在磁场中运动时，洛伦兹力提供向心力，设轨道半径为r，则有得

假设粉尘微粒从B点打出，轨道圆的圆心为O′，由r＝R可知四边形AOBO′为菱形，所以OA∥OB′，BO′一定是竖直的，速度方向与BO′垂直，因此速度方向水平向右

(2)粉尘微粒进入电场做类平抛运动，

水平方向有l＝vt    竖直方向有 

  把y≥d代入解得

19（12分）【答案】（1）0.2A（2）2m/s（3）0.1J

【解析】

试题分析：（1）导体匀速运动时：mgsinθ=f+F

F=B₀IL

f=μF_N=μmgcosθ    解得I=0.2A

（2）I=E/R

E=BLv               解得v=2m/s

（3）   解得：Q=0.1J

20（16分）【答案】（1）1．2T；1m/s²（2）18J（3）2s

【解析】试题分析：（1）经过时间t，金属棒ab的速率

回路中的感应电流为 

对金属棒ab，由牛顿第二定律得，

即   

由图b可知：t₁=0 时，F₁=11N ； t₂ = 2 s时，F₂ =14．6N  ，

代入上式解得：   

（2）在2s末金属棒ab的速率   所发生的位移

由动能定理得：

又           联立以上方程，解得：

（3）由题意可知：cd棒先做加速度逐渐减小的加速运动，当cd棒所受重力与滑动摩擦力相等时，速度达到****；然后做加速度逐渐增大的减速运动，最后停止运动。

当cd棒速度达到****时，有

又            

  v_m=at₁                        整理得