高二数学半月考(2019年10月29日)
一、单选题
1.已知命题![]() ,
,![]() .则命题
.则命题![]() 为( )
为( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
2.若![]() 为两条不同的直线,
为两条不同的直线,![]() 为平面,且
为平面,且![]() ,则“
,则“![]() ”是“
”是“![]() ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.椭圆![]() 的焦距为()
的焦距为()
A.![]() B.1 C.
B.1 C.![]() D.
D.![]()
4.下列有关命题的叙述错误的是( )
A.若非![]() 是
是![]() 的必要条件,则
的必要条件,则![]() 是非
是非![]() 的充分条件
的充分条件
B.“x>2”是“![]() ”的充分不必要条件
”的充分不必要条件
C.命题“![]() ≥0”的否定是“
≥0”的否定是“![]() <0”
<0”
D.若![]() 且
且![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
5.设抛物线![]() :
:![]() 的焦点为F,过点
的焦点为F,过点![]() 且斜率为
且斜率为![]() 的直线与
的直线与![]() 交于
交于![]() ,
,![]() 两点,则
两点,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.下列说法正确的是( )
A.向量![]() 与
与![]() 是平行向量
是平行向量
B.若![]() 都是单位向量,则
都是单位向量,则![]()
C.若![]() ,则
,则![]() 四点构成平行四边形
四点构成平行四边形
D.两向量相等的充要条件是它们的始点、终点相同
7.己知![]() ,则向量
,则向量![]() 与
与![]() 的夹角为.
的夹角为.
A.30 B.60 C.120 D.150.
8.已知双曲线![]() 的焦点到渐近线的距离为1,则渐近线方程是
的焦点到渐近线的距离为1,则渐近线方程是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.正方体![]() 中,直线
中,直线![]() 与平面
与平面![]() 所成角的正弦值为( )
所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.命题“![]() ,
,![]() ”为真命题的一个充分不必要条件是()
”为真命题的一个充分不必要条件是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
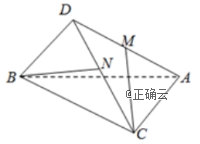
11.如图,三棱锥![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 分别为
分别为![]() 和
和![]() 的中点,则异面直线
的中点,则异面直线![]() 与
与![]() 所成角的余弦值为( )
所成角的余弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.0
D.0
12.![]() 是双曲线
是双曲线![]() 的左、右焦点,过
的左、右焦点,过![]() 的直线
的直线![]() 与
与![]() 的左、右两支分别交于
的左、右两支分别交于![]() 两点,若
两点,若![]() 为等边三角形,则双曲线
为等边三角形,则双曲线![]() 的离心率为( )
的离心率为( )
A.![]() B.
B.![]() C.2 D.3
C.2 D.3
二、填空题
13.已知“![]() ”是“
”是“![]() ”的充分不必要条件,且
”的充分不必要条件,且![]() ,则
,则![]() 的最小值是_____.
的最小值是_____.
14.若抛物线![]() 上一点到焦点和抛物线的对称轴的距离分别是10和6,则
上一点到焦点和抛物线的对称轴的距离分别是10和6,则![]() 的值为___.
的值为___.
15.给出下列结论:
①“![]() 且
且![]() 为真”是“
为真”是“![]() 或
或![]() 为真”的充分不必要条件:②“
为真”的充分不必要条件:②“![]() 且
且![]() 为假”是“
为假”是“![]() 或
或![]() 为真”的充分不必要条件;③“
为真”的充分不必要条件;③“![]() 或
或![]() 为真”是“非
为真”是“非![]() 为假”的必要不充分条件;④“非
为假”的必要不充分条件;④“非![]() 为真”是“
为真”是“![]() 且
且![]() 为假”的必要不充分条件.
为假”的必要不充分条件.
其中,正确的结论是__________.
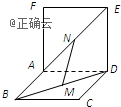
16.如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、N分别是BD和AE的中点,那么![]() ;
;![]() 面CDE;
面CDE;![]() ;
;![]() MN,CE异面其中正确结论的序号是______.
MN,CE异面其中正确结论的序号是______.
三、解答题
17.已知命题p:方程![]() 表示焦点在y轴上的椭圆;命题q:椭圆
表示焦点在y轴上的椭圆;命题q:椭圆![]() (m>0)的离心率 e∈(
(m>0)的离心率 e∈(![]() ,1),若p∨q为真,p∧q为假,求m的取值范围.
,1),若p∨q为真,p∧q为假,求m的取值范围.
18.如图,四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,且
,且![]() ,
,![]() 为
为![]() 中点.
中点.
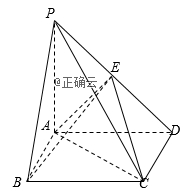
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
19.已知动点P在抛物线x2=2y上,过点P作x轴的垂线,垂足为H,动点Q满足![]() .
.
(1)求动点O的轨迹E的方程;
(2)点M(-4,4),过点N(4,5)且斜率为k的直线交轨迹E于A,B两点,设直线MA,MB的斜率分别为k1,k2,求k1k2的值.
20.如图,三棱锥P-ABC中,PA⊥平面ABC, AB⊥AC, PA=1,AB=AC=![]() ,D为BC的中点,过点D作DQ平行于AP,且DQ=1.连接QB, QC, QP.
,D为BC的中点,过点D作DQ平行于AP,且DQ=1.连接QB, QC, QP.
(Ⅰ)证明:AQ⊥平面PBC;
(Ⅱ)求直线BC与平面ABQ所成角的余弦值.
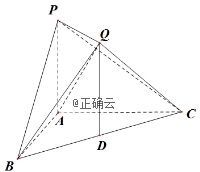
21.如图,四棱锥![]() 中,平面
中,平面![]() 底面ABCD,
底面ABCD,![]() 是等边三角形,底面ABCD为梯形,且
是等边三角形,底面ABCD为梯形,且![]() ,
,![]() ,
,![]() .
.
![]() Ⅰ
Ⅰ![]() 证明:
证明:![]() ;
;
![]() Ⅱ
Ⅱ![]() 求A到平面PBD的距离.
求A到平面PBD的距离.
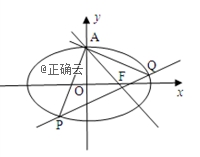
22.如图,已知椭圆![]() 的上顶点为
的上顶点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)不过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() .求证:直线
.求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.