1.【题文】函数![]() 在区间
在区间![]() 上单调递增,则的取值范围是()
上单调递增,则的取值范围是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.【题文】函数![]() 的单调递增区间是( )
的单调递增区间是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
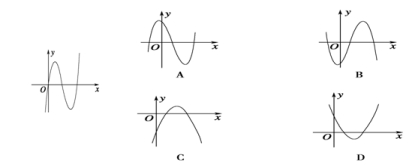
3.【题文】函数![]() 的图象如图,则导函数
的图象如图,则导函数![]() 的图象可能是( )
的图象可能是( )
4.【题文】若函数![]() 在其定义域内的一个子区间
在其定义域内的一个子区间![]() 内不是单调函数,则实数的取值范围是( )
内不是单调函数,则实数的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.【题文】函数![]() 为
为![]() 上增函数的一个充分不必要条件是()
上增函数的一个充分不必要条件是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.【题文】函数![]() 在
在![]() 上单调递增,则实数的取值范围是()
上单调递增,则实数的取值范围是()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.【题文】若![]() ,则( )
,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.【题文】若函数![]() 在
在![]() 单调递增,则的取值范围是( )
单调递增,则的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
9.【题文】函数![]() 为
为![]() 上的减函数,则实数的取值范围为____________.
上的减函数,则实数的取值范围为____________.
10.【题文】函数![]() 的单调递增区间为______________.
的单调递增区间为______________.
11.【题文】若![]() 在
在![]() 上是减函数,则b的取值范围是__________.
上是减函数,则b的取值范围是__________.
三、解答题
12.【题文】已知函数![]() ,求函数
,求函数![]() 的单调区间.
的单调区间.
13.【题文】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在区间
在区间![]() 上是减函数,求实数的取值范围.
上是减函数,求实数的取值范围.
14.【题文】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的单调区间.
的单调区间.
人教版选修2-2 课时1.3.1函数的单调性与导数
参考答案与解析
一.选择题
1.
【答案】D
【解析】![]() ,故选D.
,故选D.
考点:根据函数的单调区间求参数范围.
【题型】选择题
【难度】较易
2.
【答案】D
【解析】![]() ,由
,由![]() ,可得
,可得![]() ,所以函数
,所以函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
考点:利用导数求函数的单调区间.
【题型】选择题
【难度】较易
3.
【答案】D
【解析】由![]() 图象知,函数先增,再减,再增,对应的导数值,应该是先大于,再小于,最后大于.故选D.
图象知,函数先增,再减,再增,对应的导数值,应该是先大于,再小于,最后大于.故选D.
考点:函数单调性的图象表示.
【题型】选择题
【难度】较易
4.
【答案】B
【解析】![]() 的定义域为
的定义域为![]() ,
,![]() ,由
,由![]() ,得
,得![]() .根据题意,得
.根据题意,得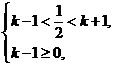 解得
解得![]() .
.
考点:由函数的单调性求参数范围.
【题型】选择题
【难度】一般
5.
【答案】B
【解析】函数![]() 为
为![]() 上增函数的充分必要条件是
上增函数的充分必要条件是![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,故选B.
,故选B.
考点:利用函数的单调性求参数范围.
【题型】选择题
【难度】一般
6.
【答案】D
【解析】若函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上恒成立,又
上恒成立,又![]() ,所以
,所以![]() .
.
考点:利用函数的单调性求参数范围.
【题型】选择题
【难度】一般
7.
【答案】B
【解析】设![]() ,所以
,所以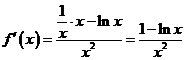 ,所以
,所以![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .则函数
.则函数![]() 在
在![]() 上单调递减.因为
上单调递减.因为![]() ,所以
,所以![]() .故选B.
.故选B.
考点:利用导数求函数单调性并比较大小.
【题型】选择题
【难度】一般
8.
【答案】C
【解析】函数在![]() 单调递增
单调递增
![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,![]() ,所以
,所以![]() .
.
考点:导数与单调区间.
【题型】选择题
【难度】较难
二、填空题
9.
【答案】![]()
【解析】![]() ,因为函数
,因为函数![]() 为
为![]() 上的减函数,所以
上的减函数,所以![]()
![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 恒成立.
恒成立.![]() ,所以
,所以![]() .
.
考点:利用函数的单调性求参数范围.
【题型】填空题
【难度】一般
10.
【答案】![]()
【解析】函数的定义域为![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() ,所以函数
,所以函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
考点:利用导数求函数的单调区间.
【题型】填空题
【难度】一般
11.
【答案】![]()
【解析】由题意可知![]() ,在
,在![]() 上恒成立
上恒成立
即![]() 在
在![]() 上恒成立,
上恒成立,![]() 且
且![]()
![]() 要使
要使![]() 恒成立,需
恒成立,需 ![]() 故答案为
故答案为![]()
考点:导数在单调性上的应用.
【题型】填空题
【难度】一般
三、解答题
12.
【答案】单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]()
【解析】![]() 令
令![]() ,即
,即![]() ,
,
解得![]() 当
当![]() ,或
,或![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
故![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,
,
单调减区间为![]() .
.
考点:利用导数求函数的单调区间.
【题型】解答题
【难度】一般
13.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】(1)当![]() 时,
时,![]() ,
,
则![]() ,所以
,所以![]() .又
.又![]() ,
,
所以所求切线方程为![]() ,即
,即![]() .
.
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)![]() ,
,
令![]() ,得
,得![]() 或
或![]() .
.
当![]() 时,
时,![]() 恒成立,不符合题意.
恒成立,不符合题意.
当![]() 时,
时,![]() 的单调递减区间是
的单调递减区间是![]() ,若
,若![]() 在区间
在区间![]() 上是减函数,
上是减函数,
则![]() 解得
解得![]() .
.
当![]() 时,
时,![]() 的单调递减区间是
的单调递减区间是![]() ,若
,若![]() 在区间
在区间![]() 上是减函数,
上是减函数,
则![]() 解得
解得![]() .
.
综上所述,实数的取值范围是![]() 或
或![]() .
.
考点:导数的几何意义,函数的导数与单调性.
【题型】解答题
【难度】一般
14.
【答案】(1)![]() (2)①当
(2)①当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,当
,当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() ,当
,当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,
,![]() 的单调递减区间是
的单调递减区间是![]() ,当
,当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]()
【解析】(1)当![]() 时,
时,![]() ,
,
![]() ,
,
![]() 函数
函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)易知函数![]() 的定义域为
的定义域为![]() ,
,![]()
![]() ,
,
令![]() ,解得
,解得![]() ,①当
,①当![]() 时,
时,![]() 恒成立,则函数
恒成立,则函数![]() 的单调递增区间是
的单调递增区间是![]() .
.
②当![]() ,即
,即![]() 时,在区间
时,在区间![]() 和
和![]() 上
上![]() ;在区间
;在区间![]() 上
上![]() ,故函数
,故函数![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() .
.
③当![]() ,即
,即![]() 时,在区间
时,在区间![]() 和
和![]() 上,
上,![]() ;在区间
;在区间![]() 上
上![]() ,故函数
,故函数![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() .
.
④当![]() ,即
,即![]() 时,在区间
时,在区间![]() 上
上![]() ,在区间
,在区间![]() 上
上![]() ,故函数
,故函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
考点:利用导数求曲线的切线方程,利用导数研究函数的单调性.
【题型】解答题
【难度】较难