1.【题文】复数z满足1-z+2i-(3-i)=2i,则z=( )
A.1-i B.-2+i
C.-2+2i D.-2+i
2.【题文】复数z1=a+4i,z2=-3+bi,若它们的和为实数,差为纯虚数,
则实数a,b的值为( )
A.a=-3,b=-4 B.a=-3,b=4
C.a=3,b=-4 D.a=3,b=4
3.【题文】若复数z满足(3-4i)z=|4+3i|,则z的虚部为( )
A.-4 B.![]() C.4 D.
C.4 D.![]()
4.【题文】已知复数![]() ,则
,则![]() ()
()
A.2 B.-2 C. 2i D.-2i
5.【题文】已知复数满足![]() ,则
,则![]() ()
()
A.![]() B.
B.![]() C.
C.![]() D. 2
D. 2
6.【题文】若复数![]() ,则
,则![]() 等于( )
等于( )
7.【题文】复数![]() (i为虚数单位)的虚部是( )
(i为虚数单位)的虚部是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.【题文】已知![]() (
(![]() ),其中为虚数单位,则
),其中为虚数单位,则![]() ()
()
A.![]() B.1 C.2 D.3
B.1 C.2 D.3
二、填空题
9.【题文】当![]() 时,z2 014+z2 016=________.
时,z2 014+z2 016=________.
10.【题文】已知是虚数单位,则复数![]() 的共轭复数是_______.
的共轭复数是_______.
11.【题文】A、B分别是复数z1、z2在复平面上对应的点,O是原点,若
|z1+z2|=|z1-z2|,则△AOB的形状是________.
三、解答题
12.【题文】计算:(1)(1+2i)+(3-4i)-(5+6i); (2)5i-(3+4i)-(-1+3i)];
(3)(a+bi)-(2a-3bi)-3i(a、b∈R).
13.【题文】已知为复数,且![]() (为虚数单位),求.
(为虚数单位),求.
14.【题文】已知![]() .
.
(1)如果![]() 求
求![]() 的值;
的值;
(2)如果![]() 求实数
求实数![]() 的值.
的值.
人教版选修1-2 课时3.2复数代数形式的四则运算
参考答案与解析
一、选择题
1.
【答案】B
【解析】z=1+2i-3+i-2i=-2+i.故选B.
考点:复数的加减运算.
【题型】选择题
【难度】较易
2.
【答案】A
【解析】由题意可知z1+z2=(a-3)+(b+4)i是实数,z1-z2=(a+3)+(4-b)i是纯虚数,故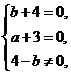 解得a=-3,b=-4,故选A.
解得a=-3,b=-4,故选A.
考点:复数的实部与虚部.
【题型】选择题
【难度】较易
3.
【答案】D
【解析】∵(3-4i)z=|4+3i|,∴![]() ,∴z的虚部为
,∴z的虚部为![]() .
.
考点:复数的除法运算.
【题型】选择题
【难度】较易
4.
【答案】A
【解析】![]() ,故选A.
,故选A.
考点:复数的基本运算.
【题型】选择题
【难度】较易
5.
【答案】A
【解析】![]() ,则
,则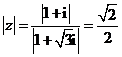 ,故选A.
,故选A.
考点:复数的运算,复数的模.
【题型】选择题
【难度】一般
6.
【答案】B
【解析】复数![]() ,则
,则![]() ,∴
,∴![]() ,故选B.
,故选B.
考点:复数的运算.
【题型】选择题
【难度】一般
7.
【答案】B
【解析】![]() ,∴虚部是
,∴虚部是![]() .
.
考点:复数的运算.
【题型】选择题
【难度】一般
8.
【答案】B
【解析】由题意,得![]() ,即
,即![]() ,所以
,所以![]() ,
,
所以![]() ,故选B.
,故选B.
考点:复数的运算.
【题型】选择题
【难度】一般
二、填空题
9.
【答案】1+ i
【解析】因为![]() ,∴
,∴![]() ,∴z2 014=(-i)1 007=i,
,∴z2 014=(-i)1 007=i,
z2 016=(-i)1 008=1,∴z2 014+z2 016=1+ i.
考点:复数的乘方运算.
【题型】填空题
【难度】较易
10.
【答案】![]()
【解析】![]() ,
,
故复数z的共轭复数是![]() .
.
考点:共轭复数的概念,复数的除法.
【题型】填空题
【难度】一般
11.
【答案】直角三角形
【解析】由|z1+z2|=|z1-z2|知,以OA、OB为邻边的平行四边形是矩形,即OA⊥OB,故△AOB是直角三角形.
考点:复数的加减运算及几何意义.
【题型】填空题
【难度】一般
三、解答题
12.
【答案】见解析
【解析】(1)(1+2i)+(3-4i)-(5+6i)=(1+3-5)+(2-4-6)i=-1-8i.
(2)5i-(3+4i)-(-1+3i)]=5i-(4+i)=-4+4i.
(3)(a+bi)-(2a-3bi)-3i=(a-2a)+b-(-3b)-3]i=-a+(4b-3)i.
考点:复数的加减运算.
【题型】解答题
【难度】较易
13.
【答案】![]()
【解析】设![]() ,则
,则![]() ,
,![]() ,代入
,代入![]() ,得
,得![]()
根据复数相等的条件可得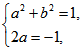 解得
解得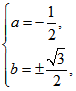
所以复数![]() .
.
考点:复数的运算.
【题型】解答题
【难度】一般
14.
【答案】(1)![]() (2)
(2)![]()
【解析】(1)因为![]() ,
,
所以![]() .
.
(2)由![]() ,得
,得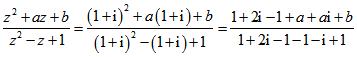
=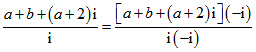 =
=![]() ,
,
因为![]() ,所以
,所以![]() =
=![]() ,
,
所以![]() 解得
解得![]()
考点:复数的四则运算、复数相等与共轭复数的概念.
【题型】解答题
【难度】一般