1．【题文】用反证法证明命题：“三角形的内角至少有一个不大于60度”时，反设正确的是（  ）

A．假设三内角都不大于60度             B．假设三内角都大于60度

C．假设三内角至多有一个大于60度    D．假设三内角至多有两个大于60度

 

2．【题文】用反证法证明“如果，那么”，假设的内容应是（）

A．                 B．且

C．                 D．或

 

3．【题文】用反证法证明命题“设为实数，则方程至少有一个实根”时，要做的假设是（）

A．方程没有实根      B．方程至多有一个实根

C．方程至多有两个实根 D．方程恰好有两个实根

 

4．【题文】用反证法证明命题“，如果可以被5整除，那么，至少有1个能被5整除．”假设的内容是（   ）

A．，都能被5整除       B．，都不能被5整除

C．不能被5整除           D．，有1个不能被5整除

 

5．【题文】用反证法证明数学命题时，首先应该做出与命题结论相反的假设．否定“自然数中恰有一个偶数”时正确的假设为（）

A．自然数都是奇数

B．自然数都是偶数

C．自然数中至少有两个偶数

D．自然数中至少有两个偶数或都是奇数

 

6．【题文】用反证法证明命题“设a，b为实数，则方程x³＋ax＋b＝0至少有一个实根”时，要做的假设是  (    )

A．方程x³＋ax＋b＝0没有实根

 B．方程x³＋ax＋b＝0至多有一个实根

C．方程x³＋ax＋b＝0至多有两个实根

D．方程x³＋ax＋b＝0恰有两个实根

 

7．【题文】已知α∩β＝l，a⊂α，b⊂β，若a，b为异面直线，则 (    )

A．a，b都与l相交                  B．a，b至少有一条与l相交

C．a，b至多有一条与l相交           D．a，b都与l不相交

 

8．【题文】设椭圆(a＞b＞0)的离心率为e＝，右焦点为F(c，0)，方程ax²＋bx－c＝0的两个实根分别为x₁和x₂，则点P(x₁，x₂)(    )

A．必在圆x²＋y²＝2上                B．必在圆x²＋y²＝2外

C．必在圆x²＋y²＝2内                D．以上三种情形都有可能

 

二、填空题

9．【题文】用反证法证明命题“若，则或”时，应假设

__________________________.

 

10．【题文】用反证法证明命题：“设实数a、b、c满足a＋b＋c＝1，则a、b、c中至少有一个数不小于”时，第一步应写：假设_______________________．

 

11．【题文】用反证法证明“一个三角形不能有两个直角”有三个步骤：

①∠A＋∠B＋∠C＝90°＋90°＋∠C＞180°，这与三角形内角和为180°矛盾，故假设错误．

②所以一个三角形不能有两个直角．

③假设△ABC中有两个直角，不妨设∠A＝90°，∠B＝90°.上述步骤的正确顺序为________．

 

三、解答题

12．【题文】已知正数成等差数列，且公差，用反证法求证：不可能是等差数列.

 

13．【题文】（1）求证：；

（2）已知且，求证：中至少有一个小于2.

 

14．【题文】已知函数．

（1）证明：函数f(x)在(－1，＋∞)上为增函数；

（2）用反证法证明方程f(x)＝0没有负数根．

 

人教版选修1-2 课时2.2.2反证法

参考答案与解析

一、选择题

1． 

【答案】B

【解析】由反证法的证明命题的格式和语言可知答案B是正确的，所以选B.

考点：反证法的反设.

【题型】选择题

【难度】较易

2． 

【答案】D

【解析】原命题的结论为，反证法需假设结论的反面，应为小于或等于，即或.

考点：反证法的假设环节.

【题型】选择题

【难度】较易

3． 

【答案】A

【解析】方程至少有一个实根的否定是方程没有实根，用反证法证明命题“设为实数，则方程至少有一个实根”时，要做的假设是方程没有实根．故选A．

考点：反证法假设环节．

【题型】选择题

【难度】较易

4． 

【答案】B

【解析】用反证法证明时，要假设所要证明的结论的反面成立，本题中应反设，都不能被5整除.

考点：反证法的假设环节.

【题型】选择题

【难度】较易

5． 

【答案】D

【解析】反证法证明时应假设所要证明的结论的反面成立，本题需反设为自然数中至少有两个偶数或都是奇数.

考点：反证法.

【题型】选择题

【难度】较易

6． 

【答案】A

【解析】因为“方程x³＋ax＋b＝0至少有一个实根”等价于“方程x³＋ax＋b＝0的实根个数大于或等于1”，所以假设是“方程x³＋ax＋b＝0没有实根”．

考点：反证法的假设.

【题型】选择题

【难度】一般

7． 

【答案】B

【解析】若a，b都与l不相交，则a∥l，b∥l，∴a∥b，这与a，b为异面直线矛盾，∴a，b至少有一条与l相交．故选B.

考点：反证法.

【题型】选择题

【难度】一般

8． 

【答案】C

【解析】∵，∴a＝2c，∴b²＝a²－c²＝3c².假设点P(x₁，x₂)不在圆

x²＋y²＝2内，则，但

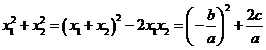
，矛盾．

∴假设不成立．∴点P必在圆x²＋y²＝2内．故选C.

考点：反证法.

【题型】选择题

【难度】较难

二、填空题

9． 

【答案】且

【解析】反证法的反设只否定结论，或的否定是且，所以是且.

考点：反证法.

【题型】填空题

【难度】较易

10． 

【答案】都小于

【解析】反证法第一步是否定结论，a、b、c中至少有一个数不小于的否定是都小于．

考点：反证法.

【题型】填空题

【难度】较易

11． 

【答案】③①②

【解析】由反证法证明数学命题的步骤可知，步骤的顺序应为③①②.

考点：反证法.

【题型】填空题

【难度】一般

三、解答题

12． 

【答案】见解析

【解析】证明：假设成等差数列，则，即两边乘以b，得，又∵a，b，c成等差数列，且公差不为零，

∴．∴．两边都乘以ac，得a=c．

这与已知数列a，b，c的公差不为零，a≠c相矛盾，

所以数列不可能成等差数列.

考点：反证法.

【题型】解答题

【难度】一般

13． 

【答案】（1）证明见解析（2）证明见解析

【解析】（1）因为和都是正数，所以欲证，

只需证，只需证，即证，

即证，即证，因为显然成立，所以原不等式成立.

（2）证明：假设都不小于2，则，

因为，

这与已知矛盾，故假设不成立，从而原结论成立.

考点：分析法与反证法.

【题型】解答题

【难度】一般

14． 

【答案】（1）证明见解析（2）证明见解析

【解析】（1）证法一：任取，不妨设，则，且，所以，

又因为，所以，

于是，

故函数在(－1，＋∞)上为增函数．

证法二：，，

在上恒成立，即在上为增函数．

（2）设存在满足，则，且，

所以，解得，与假设矛盾．

故方程没有负数根．

考点：函数的单调性，反证法.

【题型】解答题

【难度】较难