1.【题文】某箱子的容积与底面边长x的关系为![]() ,则当箱子的容积****时,箱子的底面边长为( )
,则当箱子的容积****时,箱子的底面边长为( )
A.30 B.40 C.50 D.35
2.【题文】已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为![]() ,则使该生产厂家获取****年利润的年产量为( )
,则使该生产厂家获取****年利润的年产量为( )
A.13万件 B.11万件
C.9万件 D.7万件
3.【题文】路灯距地平面8 m,一个身高为1.6 m的人以2 m/s的速度在地平面上,从路灯在地平面上的射影点C开始沿某直线离开路灯,那么人影长度的变化速度v为()
A.![]() m/s B.
m/s B.![]() m/s C.
m/s C.![]() m/s D.
m/s D.![]() m/s
m/s
4.【题文】现有一段长为18 m的铁丝,要把它围成一个底面一边长为另一边长2倍的长方体形状的框架,当长方体体积****时,底面的较短边长是()
A.1 m B.1.5 m C.0.75 m D.0.5 m
5.【题文】某公司规定:对于小于或等于150件的订购合同,每件售价为200元,对于多于150件的订购合同,每超过一件,则每件的售价比原来减少1元,则使公司的收益****时应该订购的合同件数是( )
A. 150 B. 175 C. 200 D. 225
6.【题文】用边长为120 cm的正方形铁皮做一个无盖水箱,先在四角分别截去一个小正方形,然后把四边翻转90°,焊接成水箱,则水箱的****容积为( )
A.120 000 cm3 B.128 000 cm3
C.150 000 cm3 D.158 000 cm3
7.【题文】某产品的销售收入y1(万元)关于产量x(千台)的函数为y1=17x2(x>0);生产成本y2(万元)关于产量x(千台)的函数为y2=2x3-x2(x>0),为使利润****,应生产( )
A.6千台 B.7千台 C.8千台 D.9千台
8.【题文】某工厂需要建一个面积为512 m2的矩形堆料场,一边可以利用原有的墙壁,要使砌墙所用材料最省,堆料场的长和宽分别为( )
A.16 m,16 m B.32 m,16 m
C.32 m,8 m D.16 m,8 m
二、填空题
9.【题文】要做一个底面为长方形的带盖的箱子,其体积为72 cm3,其底面两邻边长之比为1∶2,则它的长为______,宽为______,高为______时,可使表面积最小.
10.【题文】某商品一件的成本为30元,在某段时间内以每件x元出售,可卖出(200-x)件,要使利润****,每件定价为_______元.
11.【题文】已知某厂生产(百件)某种商品的总成本为![]()
![]() (万元),总收益为
(万元),总收益为![]() (万元),则生产这种商品所获利润的****值为__________万元,此时生产这种商品____________百件.
(万元),则生产这种商品所获利润的****值为__________万元,此时生产这种商品____________百件.
三、解答题
12.【题文】已知某厂生产件产品的成本为![]() (元),问:(1)要使平均成本最低,应生产多少件产品?
(元),问:(1)要使平均成本最低,应生产多少件产品?
(2)若产品以每件![]() 元售出,要使利润****,应生产多少件产品?
元售出,要使利润****,应生产多少件产品?
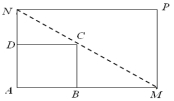
13.【题文】为了美化城市,某市将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,如图所示.要求B在AM上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米.
(1)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(2)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
14.【题文】某地开发了一个旅游景点,第1年的游客约为100万人,第2年的游客约为120万人.某数学兴趣小组综合各种因素预测:①该景点每年的游客人数会逐年增加;②该景点每年的游客都达不到130万人.该兴趣小组想找一个函数![]() 来拟合该景点对外开放的第
来拟合该景点对外开放的第![]() 年与当年的游客人数
年与当年的游客人数![]() (单位:万人)之间的关系.
(单位:万人)之间的关系.
(1)根据上述两点预测,请用数学语言描述函数![]() 所具有的性质;
所具有的性质;
(2)若![]() =
=![]() ,试确定
,试确定![]() 的值,并说明该函数是否符合上述两点预测;
的值,并说明该函数是否符合上述两点预测;
(3)若![]() =
=![]() ,欲使得该函数符合上述两点预测,试确定的取值范围.
,欲使得该函数符合上述两点预测,试确定的取值范围.
人教版选修1-1 课时3.4生活中的优化问题举例
参考答案与解析
一、选择题
1.
【答案】B
【解析】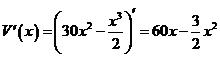 ,x∈(0,60).令V′(x)=0,
,x∈(0,60).令V′(x)=0,
得x=40. ∴当x=40时,箱子的容积有****值.
考点:体积****问题.
【题型】选择题
【难度】较易
2.
【答案】C
【解析】y′=-x2+81,令y′=0,得x=9或x=-9(舍去).当0<x<9时,y′>0;当x>9时,y′<0,故当x=9时,函数有极大值,也是****值.
考点:利润****问题.
【题型】选择题
【难度】较易
3.
【答案】D
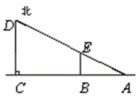
【解析】如图,设人从C点运动到B处路程为x m,时间为t s,AB为人影长度,AB长为y m.由于DC∥BE,则![]() ,即
,即![]() .
.
∴y=![]() x=
x=![]() t,∴v=y′=
t,∴v=y′=![]() m/s.
m/s.
考点:速度问题.
【题型】选择题
【难度】较易
4.
【答案】A
【解析】设长方体底面较短边的长为x m,则较长边的长为2x m,高为![]() =
=![]() m,它的体积为
m,它的体积为![]() (其中0<x<
(其中0<x<![]() ).对V求导,并令V′=0,得18x−18x2=0,解得x=0,或x=1.当0<x<1时,函数V单调递增,当1<x<
).对V求导,并令V′=0,得18x−18x2=0,解得x=0,或x=1.当0<x<1时,函数V单调递增,当1<x<![]() 时,函数V单调递减,所以当x=1时,函数V有****值.因此底面的较短边长是1 m,故选A.
时,函数V单调递减,所以当x=1时,函数V有****值.因此底面的较短边长是1 m,故选A.
考点:体积****问题.
【题型】选择题
【难度】一般
5.
【答案】B
【解析】设x表示订购的件数,R表示公司的收益,则R等于每件的售价×订购的件数x,当x≤150时,R=200x,****收益为200×150=30 000元;当x>150时,R=200-(x-150)]x=350x-x2,R′=350-2x,令R′=0,得x=175,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,则当x=175时,R有****值,****收益为350×175-1752=30 625元,故选B.
,则当x=175时,R有****值,****收益为350×175-1752=30 625元,故选B.
考点:利润****问题.
【题型】选择题
【难度】一般
6.
【答案】B
【解析】设水箱的高为x cm(0<x<60),则水箱底面边长为(120-2x)cm,水箱的容积V=(120-2x)2·x=(1202-480x+4x2)·x,∴V′=12x2-960x+120×120,令V′=0,得x=20或x=60(舍去).当0<x<20时,V′>0;当20<x<60时,V′<0.∴当x=20时,V有****值,且****值为128 000 cm3.
考点:体积****问题.
【题型】选择题
【难度】一般
7.
【答案】A
【解析】设利润为y万元,则y=y1-y2=17x2-2x3+x2=18x2-2x3(x>0),y′=36x-6x2,令y′>0,得0<x<6,令y′<0,得x>6,∴当x=6时,y取****值,故为使利润****,应生产6千台.
考点:利润****问题.
【题型】选择题
【难度】一般
8.
【答案】B
【解析】如图所示,设场地垂直于墙的一边长为x m,则其邻边长为![]() m.
m.
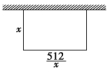
因此新墙总长度![]() ,
,![]() .令L′=0,得x=16或x=-16(舍去).可知当x=16时,L取得最小值,当x=16时,
.令L′=0,得x=16或x=-16(舍去).可知当x=16时,L取得最小值,当x=16时,![]() .故当堆料场的宽为16 m,长为32 m时,可使砌墙所用的材料最省.
.故当堆料场的宽为16 m,长为32 m时,可使砌墙所用的材料最省.
考点:材料最省问题.
【题型】选择题
【难度】一般
二、填空题
9.
【答案】6 cm;3 cm;4cm
【解析】设底面相邻两边长分别为x cm、2x cm,高为y cm.
则V=2x2y=72,y=![]() =
=![]() ,S=2(2x2+2xy+xy)=4x2+6xy=4x2+
,S=2(2x2+2xy+xy)=4x2+6xy=4x2+![]() .
.
S′=8x-![]() ,令S′=0,解得x=3.
,令S′=0,解得x=3.
则长为6 cm,宽为3 cm,高为4 cm时,表面积最小.
考点:表面积最小问题.
【题型】填空题
【难度】一般
10.
【答案】115
【解析】依题意可得利润为L=(x-30)(200-x)=-x2+230x-6 000(0<x<200).
L′=-2x+230,令L′=-2x+230=0,解得![]() .
.
因为在(0,200)内L只有一个极值,所以以每件115元出售时利润****.
考点:利润****问题.
【题型】填空题
【难度】一般
11.
【答案】66;9
【解析】设利润为![]() (万元),
(万元),
则![]()
![]() ,
,
∴![]() ,由
,由![]() 得
得![]() ,
,
∴![]() 时,
时,![]() 单调递增,
单调递增,![]() 时,
时,![]() 单调递减,∴
单调递减,∴![]() 时,
时,![]() 有****值
有****值![]()
考点:利润****问题.
【题型】填空题
【难度】一般
三、解答题
12.
【答案】(1)![]() 件(2)
件(2)![]() 件
件
【解析】(1)设平均每件的成本为![]() 元,
元,
则
![]() ,∴
,∴![]() .令
.令![]() ,得
,得![]() 或
或![]() (舍去),可知当
(舍去),可知当![]() 时,函数取得极小值且为最小值,所以要使平均成本最小,应生产
时,函数取得极小值且为最小值,所以要使平均成本最小,应生产![]() 件产品.
件产品.
(2)设利润为元,则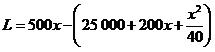
![]() ,
,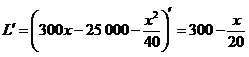 ,令
,令![]() ,得
,得![]() ,可知当
,可知当![]() 时
时![]() 取得极大值且为****值,因此要使利润****,应生产
取得极大值且为****值,因此要使利润****,应生产![]() 件产品.
件产品.
考点:利润****问题.
【题型】解答题
【难度】一般
13.
【答案】(1)![]() (单位:米) (2) |AN|=6米,|AM|=4.5米,最小面积为27平方米
(单位:米) (2) |AN|=6米,|AM|=4.5米,最小面积为27平方米
【解析】设AN的长为x米(x>2),易得![]() ,∴
,∴![]() ,
,
∴![]() .
.
(1)由![]() 得
得![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
即![]() ,∴
,∴![]() 或
或![]() ,即AN长的取值范围是
,即AN长的取值范围是![]() (单位:米).
(单位:米).
(2)令![]() ,则
,则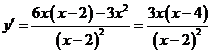 ,
,
∴当![]() 时,
时,![]() ,即函数
,即函数![]() 在
在![]() 上单调递增,
上单调递增,
∴函数![]() 上单调递增,
上单调递增,
∴当x=6时,![]() 取得最小值,即
取得最小值,即![]() 取得最小值,为27(平方米).此时|AN|=6米,|AM|=4.5米.故当AM、AN的长度分别是4.5米,6米时,矩形AMPN的面积最小,最小面积是27平方米.
取得最小值,为27(平方米).此时|AN|=6米,|AM|=4.5米.故当AM、AN的长度分别是4.5米,6米时,矩形AMPN的面积最小,最小面积是27平方米.
考点:面积最小问题.
【题型】解答题
【难度】一般
14.
【答案】(1)详见解析(2)详见解析(3)![]()
【解析】(1)根据题中两点预测可知![]() 在
在![]() 上单调递增,
上单调递增,![]() 对
对![]() 恒成立.
恒成立.
(2)将(1,100),(2,120)代入![]() 中,得
中,得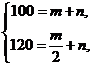 解得
解得![]()
所以![]() ,所以
,所以![]() ,
,
故![]() 在
在![]() 上单调递增,符合预测①;
上单调递增,符合预测①;
又当![]() 时,
时,![]() ,所以此时
,所以此时![]() 不符合预测②.
不符合预测②.
(3)由![]() 解得
解得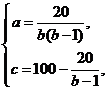
![]() ,要想符合预测①,则有
,要想符合预测①,则有![]() ,
,
即![]() ,从而
,从而![]() 或
或![]()
当![]() 时,
时,![]() ,此时符合预测①.由
,此时符合预测①.由![]() ,解得
,解得![]() ,
,
即当![]() 时,
时,![]() ,所以此时
,所以此时![]() 不符合预测②;
不符合预测②;
当![]() ,
,![]() ,此时符合预测①,又由
,此时符合预测①,又由![]() ,知
,知![]() ,所以
,所以![]() ,从而
,从而![]() .
.
欲使![]() 也符合预测②,则
也符合预测②,则![]() ,即
,即![]() ,又
,又![]() ,解得
,解得![]() .综上所述,的取值范围是
.综上所述,的取值范围是![]() .
.
考点:函数在实际问题中的应用,导数的应用.
【难度】较难