1.【题文】定义在闭区间a,b]上的函数y=f(x)有****的极值点x=x0,且y极小值=f(x0),则下列说法正确的是( )
A.函数f(x)有最小值f(x0)
B.函数f(x)有最小值,但不一定是f(x0)
C.函数f(x)的****值也可能是f(x0)
D.函数f(x)不一定有最小值
2.【题文】函数f(x)=x3-3x(|x|<1)( )
A.有****值,但无最小值 B.有****值,也有最小值
C.无****值,但有最小值 D.既无****值,也无最小值
3.【题文】函数y=2x3-3x2-12x+5在-2,1]上的****值,最小值分别是( )
A.12,-8 B.1,-8
C.12,-15 D.5,-16
4.【题文】已知f(x)=![]() x2-cosx,x∈-1,1],则导函数f′(x)是( )
x2-cosx,x∈-1,1],则导函数f′(x)是( )
A.仅有最小值的奇函数
B.既有****值又有最小值的偶函数
C.仅有****值的偶函数
D.既有****值又有最小值的奇函数
5.【题文】已知![]() (m为常数)在区间
(m为常数)在区间![]() 上有****值3,那么此函数在
上有****值3,那么此函数在![]() 上的最小值为 ( )
上的最小值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.【题文】函数![]() ,若对于区间-3,2]上的任意x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是( )
,若对于区间-3,2]上的任意x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是( )
A.20 B.18 C.3 D.0
7.【题文】若函数![]() ,则( )
,则( )
A.****值为,最小值为![]() B.****值为,无最小值
B.****值为,无最小值
C.最小值为![]() ,无****值 D.既无****值也无最小值
,无****值 D.既无****值也无最小值
8.【题文】函数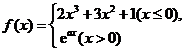 在
在![]() 上的****值为2,则a的取值范围是( )
上的****值为2,则a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
9.【题文】函数![]() 在
在![]() 上的最小值是__________.
上的最小值是__________.
10.【题文】函数f(x)=x(1-x2)在0,1]上的****值为__________.
11.【题文】函数![]() 在
在![]() 上的最小值为______.
上的最小值为______.
三、解答题
12.【题文】已知函数![]() ,
,![]() .若
.若![]() 的图象在
的图象在![]() 处与直线
处与直线![]() 相切.
相切.
(1)求![]() 的值;
的值;
(2)求![]() 在
在![]() 上的****值.
上的****值.
13.【题文】函数![]()
(1)若函数![]() 在
在![]() 内没有极值点,求的取值范围;
内没有极值点,求的取值范围;
(2)若对任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
14.【题文】已知函数![]() ,
,
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值.
上的最小值.
人教版选修1-1 课时3.3.3 函数的****(小)值与导数
参考答案与解析
一、选择题
1.
【答案】A
【解析】函数f(x)在闭区间a,b]上一定存在****值和最小值,又f(x)有****的极小值f(x0),则f(x0)一定是最小值.
考点:函数最值的判断.
【题型】选择题
【难度】较易
2.
【答案】D
【解析】f ′(x)=3x2-3=3(x+1)(x-1),∵x∈(-1,1),∴f ′(x)<0,即函数在
(-1,1)上是递减的,∴函数f(x)在区间(-1,1)上既无****值,也无最小值.
考点:利用导数判断函数的最值.
【题型】选择题
【难度】较易
3.
【答案】A
【解析】y′=6x2-6x-12,由y′=0⇒x=-1或x=2(舍去).当x=-2时,y=1;当x=-1时,y=12;当x=1时,y=-8.∴ymax=12,ymin=
-8.故选A.
考点:利用导数求函数在闭区间上的最值.
【题型】选择题
【难度】较易
4.
【答案】D
【解析】求导可得f′(x)=x+sinx,显然f′(x)是奇函数,令h(x)=f′(x),
则h(x)=x+sinx,求导得h′(x)=1+cosx,当x∈-1,1]时,h′(x)>0,
所以h(x)在-1,1]上单调递增,有****值和最小值.
所以f′(x)是既有****值又有最小值的奇函数.
考点:函数最值与奇偶性.
【题型】选择题
【难度】一般
5.
【答案】D
【解析】令![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以****值在
,所以****值在![]() 处取得,即
处取得,即![]() ,又
,又![]() ,所以最小值为
,所以最小值为![]() .
.
考点:用导数求函数在闭区间上的最值.
【题型】选择题
【难度】一般
6.
【答案】A
【解析】![]() ,所以
,所以![]() 在区间
在区间![]() ,
,![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.![]() ,
,![]() ,
,![]() ,
,![]() ,可知
,可知![]() 的****值为20,故的最小值为20.
的****值为20,故的最小值为20.
考点:利用导数求函数的单调性与最值.
【题型】选择题
【难度】一般
7.
【答案】D
【解析】![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,令
,令![]() ,得
,得![]() ,因此函数
,因此函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以在
上单调递增,所以在![]() 时,函数
时,函数![]() 取得极大值,在
取得极大值,在![]() 时,函数
时,函数![]() 取得极小值
取得极小值![]() ,但是函数
,但是函数![]() 在
在![]() 上,既无****值也无最小值,故选D.
上,既无****值也无最小值,故选D.
考点:导数的应用、函数的极值与最值.
【题型】选择题
【难度】一般
8.
【答案】D
【解析】当![]() 时,
时,![]() ,令
,令![]() 得
得![]() ,令
,令![]() ,得
,得![]() ,则在
,则在![]() 上的****值为
上的****值为![]() .欲使得函数
.欲使得函数![]() 在
在![]() 上的****值为2,则当
上的****值为2,则当![]() 时,
时,![]() 的值必须小于或等于2,即
的值必须小于或等于2,即![]() ,解得
,解得![]() ,故选D.
,故选D.
考点:函数最值的应用.
【题型】选择题
【难度】较难
二、填空题
9.
【答案】
【解析】![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,从而函数
上单调递增,从而函数![]() 在
在![]() 上的最小值是
上的最小值是![]() .
.
考点:利用导数求函数在闭区间上的最值.
【题型】填空题
【难度】较易
10.
【答案】![]()
【解析】由题知![]() ,则
,则![]() ,可得在区间
,可得在区间![]() 上,
上,![]() ,
,![]() 为增函数,在
为增函数,在![]() 上,
上,![]() ,
,![]() 为减函数,故
为减函数,故![]() 在
在![]() 处取得****值
处取得****值![]() .
.
考点:由导函数求函数在闭区间的最值.
【题型】填空题
【难度】一般
11.
【答案】![]()
【解析】![]() ,令
,令![]() ,得
,得![]() .列表如下:
.列表如下:
|
|
|
0 |
(0,1) |
1 |
(1,2) |
2 | |
|
|
0 |
+ |
0 |
0 |
+ |
||
|
|
|
增 |
|
减 |
|
增 |
3 |
由表可知,函数的最小值为![]() .
.
考点:函数的最值及导数的应用.
【题型】解答题
【难度】一般
三、解答题
12.
【答案】(1)![]() (2)****值为
(2)****值为![]()
【解析】(1)![]() .由函数
.由函数![]() 的图象在
的图象在![]() 处与直线
处与直线![]() 相切,得
相切,得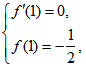 即
即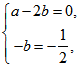 解得
解得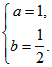
(2)由(1)得![]() ,定义域为
,定义域为![]() ,
,![]() ,令
,令![]() ,解得
,解得![]() ,令
,令![]() ,得
,得![]() .
.
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 在
在![]() 上的****值为
上的****值为![]() .
.
考点:导数的几何意义,利用导数求解函数的最值.
【题型】解答题
【难度】较易
13.
【答案】(1)![]() 或
或![]() 或
或![]() (2)
(2)![]()
【解析】(1)由题意知,![]() ,当
,当![]() 时,
时,![]() 恒成立,在定义域上没有极值,符合题意;当
恒成立,在定义域上没有极值,符合题意;当![]() 时,因为
时,因为![]() ,所以
,所以![]() 解得
解得![]() 或
或![]() .综上,
.综上,![]() 或
或![]() 或
或![]() .
.
(2)![]() ,因为
,因为![]() ,所以函数
,所以函数![]() 的递增区间为
的递增区间为![]() ,递减区间为
,递减区间为![]() .当
.当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上的****值等于
上的****值等于![]() 中****的一个,而
中****的一个,而![]() ,所以
,所以![]() ,因为
,因为![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() ,即
,即![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() .
.
考点:利用导数求闭区间上函数的最值.
【题文】解答题
【难度】一般
14.
【答案】(1)单调递增区间为![]() ,单调减区间为
,单调减区间为![]() (2)当
(2)当![]() 时,
时, ![]() ;当
;当![]() 时,
时,![]()
【解析】(1)当![]() 时,
时,![]() ,则
,则![]() (
(![]() ),
),
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() .
.
故函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(2)由![]() 得
得![]() ,
,
令![]() 得
得![]() ,令
,令![]() 得
得![]() ,
,
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
①当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间1,2]上是减函数,
在区间1,2]上是减函数,
∴![]() 的最小值是
的最小值是![]() .
.
②当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间1,2]上是增函数,
在区间1,2]上是增函数,
∴![]() 的最小值是
的最小值是![]() .
.
③当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 是减函数.又
是减函数.又![]() ,∴当
,∴当![]() 时,
时,![]() 最小值是
最小值是![]() ;当
;当![]() 时,最小值为
时,最小值为![]() .
.
综上,当![]() 时,
时, ![]() ;当
;当![]() 时,
时,![]() .
.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性.
【题型】解答题
【难度】较难