【要点解读】

直线与平面垂直：定义法：如果一条直线和一个平面内的任意一条直线都垂直，我们就说直线和平面 互相垂直.判定定理：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面。（线线垂直线面垂直）{}

面面垂直的性质定理：如果两个平面互相垂直，那么在一个平面内垂直于交线的直线垂直于另一个平面。（面面垂直线面垂直）{}

直线和平面垂直的性质：两条平行直线，若其中一条垂直于一个平面，则另一条必定也垂直于这个平面。

{}

结论：一条直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。

【考向】直线与平面垂直的判定与性质的应用

【例题】

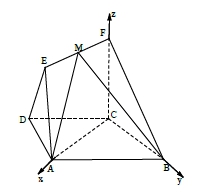
【2017届湖南长沙长郡高三入学考试】如图，在等腰梯形中，，，，四边形为矩形，平面平面，.

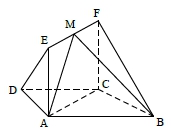
（1）求证：平面；

（2）点在线段上运动，设平面与平面二面角的平面角为，试求的取值范围.

【名师点睛】

证线面垂直的方法有：

(1)利用判定定理，它是最常用的思路．

(2)利用线面垂直的性质：若两平行线之一垂直于平面，则另一条线必垂直于该平面．

(3)利用面面垂直的性质：①两平面互相垂直，在一个面内垂直于交线的直线垂直于另一平面．

②若两相交平面都垂直于第三个平面，则它们的交线垂直于第三个平面．

（4）是平行线法(若两条平行线中一条垂直于这个平面，则另一条也垂直于这个平面)．

解题时，注意线线、线面与面面关系的相互转化；另外，在证明线线垂直时，要注意题中隐含的垂直关系，如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形(或给出线段长度，经计算满足勾股定理)、直角梯形等等．在解决直线与平面垂直的问题过程中，要注意直线与平面垂直定义，判定定理和性质定理的联合交替使用，即注意线线垂直和线面垂直的互相转化．注意以下几点：①由已知想性质，由求证想判定，即分析法与综合法相结合寻找证题思路.②立体几何论证题的解答中，利用题设条件的性质适当添加辅助线（或面）是解题的常用方法之一.③明确何时应用判定定理，何时应用性质定理，用定理时要先申明条件再由定理得出相应结论.④三垂线定理及其逆定理在高考题中使用的频率****，在证明线线垂直时应优先考虑.应用时常需先认清所观察的平面及它的垂线，从而明确斜线、射影、面内直线的位置，再根据定理由已知的两直线垂直得出新的两直线垂直.另外通过计算证明线线垂直也是常用的方法之一.

重点2：平面与平面垂直的判定与性质的应用

【要点解读】

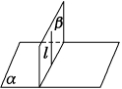
两个平面垂直的定义：相交成直二面角的两个平面叫做互相垂直的平面.

两平面垂直的判定定理：（线面垂直面面垂直）

如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直.

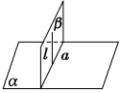
两平面垂直的性质定理：（面面垂直线面垂直）若两个平面互相垂直，那么在一个平面内垂直于它们的交线的直线垂直于另一个平面.

【考向】平面与平面垂直的判定与性质的应用

【例题】

【2017届河北石家庄市9月摸底】如图，四边形是边长为2的菱形，,分别为的中点，将沿折起，使得.

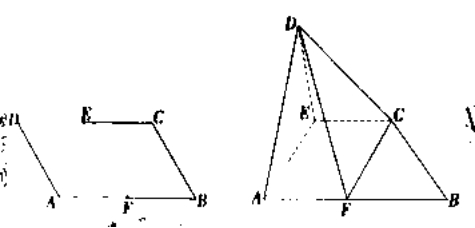
（1）求证：平面平面；

（2）求点到平面的距离.

方法（二）点到平面的距离即为点到平面的距离.又因为//,  且面,  //面,所以所求距离即为点到平面的距离，过点作,由（1）知平面平面，平面,在等腰中，，,即点到平面的距离为.

【名师点睛】

面面垂直的证明方法：①定义法；②面面垂直的判断定理；③向量法：证明两个平面的法向量垂直.解题时要由已知相性质，由求证想判定，即分析法和综合法相结合寻找证明思路，关键在于对题目中的条件的思考和分析，掌握做此类题的一般技巧和方法，以及如何巧妙进行垂直之间的转化.

证面面垂直，关键是考虑证哪条线垂直哪个面.这必须结合条件中各种垂直关系充分发挥空间想象综合考虑；条件中告诉我们某种位置关系，就要联系到相应的性质定理.已知两平面互相垂直，我们就要两平面互相垂直的性质定理；在垂直关系的证明中，线线垂直是问题的核心，可以根据已知的平面图形通过计算的方式（如勾股定理）证明线线垂直，也可以根据已知的垂直关系证明线线垂直，其中要特别重视两个平面垂直的性质定理，这个定理已知的是两个平面垂直，结论是线面垂直．

 面面垂直的性质定理是作辅助线的一个重要依据．我们要作一个平面的一条垂线，通常是先找这个平面的一个垂面，在这个垂面中，作交线的垂线即可．每一垂直的判定就是从某一垂直开始转向另一垂直最终达到目的.例如：有两个平面垂直时，一般要用性质定理，在一个平面内作交线的垂线，使之转化为线面垂直，然后进一步转化为线线垂直.

重点3：线面、面面垂直的综合应用

【要点解读】

1．直线与平面垂直

(1)判定直线和平面垂直的方法

①定义法．

②利用判定定理：如果一条直线与平面内的两条相交直线垂直，则这条直线与这个平面垂直．

③推论：如果在两条平行直线中，有一条垂直于平面，那么另一条直线也垂直于这个平面．

(2)直线和平面垂直的性质

①直线垂直于平面，则垂直于平面内任意直线．

②垂直于同一个平面的两条直线平行．

③垂直于同一直线的两平面平行．

2．斜线和平面所成的角

斜线和它在平面内的射影所成的锐角，叫斜线和平面所成的角．

3．平面与平面垂直

(1)平面与平面垂直的判定方法

①定义法

②利用判定定理：如果一个平面过另一个平面的一条垂线，则这两个平面互相垂直．

(2)平面与平面垂直的性质

如果两平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面．

【考向】线面、面面垂直的综合应用

【例题】

【2017届福建福州外国语学校高三上月考】如图，是以为直径的半圆上异于点的一点，矩形所在平面垂直于该半圆所在的平面，且．

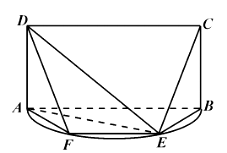
（I）求证：；

（II）设平面与半圆弧的另一个交点为，，求三棱锥的体积．

【名师点睛】

1. 垂直关系的转化：

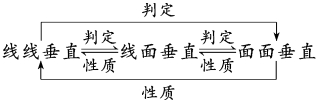
2．在证明两平面垂直时一般先从现有的直线中寻找平面的垂线，若这样的直线图中不存在，则可通过作辅助线来解决．如有平面垂直时，一般要用性质定理，在一个平面内作交线的垂线，使之转化为线面垂直，然后进一步转化为线线垂直．故熟练掌握“线线垂直”、“面面垂直”间的转化条件是解决这类问题的关键．

平行、垂直关系综合题的类型及解法

(1)三种垂直的综合问题，一般通过作辅助线进行线线、线面、面面垂直间的转化.

(2)垂直与平行结合问题，求解时应注意平行、垂直的性质及判定的综合应用.

(3)垂直与体积结合问题，在求体积时，可根据线面垂直得到表示高的线段，进而求得体积.

【趁热打铁】

1.【2017届河南新乡一中高三上学期周考】．若是两条不同的直线，是三个不同的平面，则下列为真命题的是（     ）

A．若，则    B．若，则   

C．若，则    D．若，则

2. 【2016届浙江稽阳联谊学校高三4月联考】设是两条不同的直线，是两个不同的平面，且，下列说法正确的是（    ）

A．若，则   B．若，则

C．若，则   D．若，则

3. 【2017届江西南昌市高三上学期摸底调研】正四面体中，分别是的中点，下面四个结论中不成立的是（   ）

A．平面      B．平面平面 

C．平面      D．平面平面

4. 【2017届河北衡水高三摸底联考】如图，三棱柱中,.

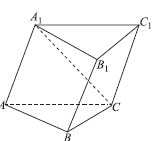
（1）证明:；

（2）若,求三棱住的体积.

5. 【2017届湖北武汉市部分学校高三上学期起点考试】如图，四棱锥中，，，△与△都是等边三角形．

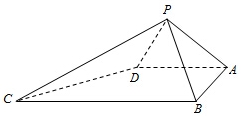
（1）证明：平面；

（2）求二面角的平面角的余弦值．

6.【2017届河南省天一大联考高三上学期段测】如图，已知等边中，，分别为，边的中点，为的中点，为边上一点，且，将沿折到的位置，使平面平面.

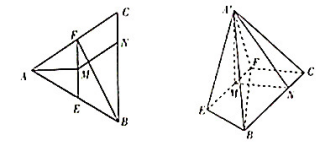
（Ⅰ）求证：平面平面；

（Ⅱ）设，求三棱锥的体积.