17、(本小题满分10分)求以原点为顶点,坐标轴为对称轴,并且经过点![]() 的抛物线的标准方程.
的抛物线的标准方程.
18、(本小题满分12分)如图所示,直线l:y=x+b与抛物线C:x2=4y相切于点A.
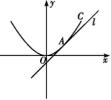
(1)求实数b的值;
(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程.
19、(本小题满分12分)椭圆C的中心为坐标原点O,焦点在y![]() 轴上,短轴长为
轴上,短轴长为![]() 、离心率为
、离心率为![]() ,直线
,直线![]() 与y轴交于点P(0,
与y轴交于点P(0,![]() ),与
),与![]() 椭圆C交于相异两点A、B,且AP=3PB。
椭圆C交于相异两点A、B,且AP=3PB。
(1)求椭圆方程;
(2)求![]() 的取值范围。
的取值范围。
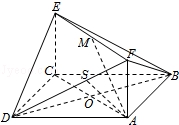
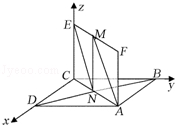
20、(本小题满分12分)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=![]() ,AF=1,
,AF=1,
M是线段EF的中点.
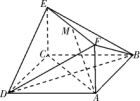
(1)求证:AM∥平面BDE;
(2)求二面角A-DF-B的大小;
(3)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
21、(本小题满分12分)设关于x的一元二次方程x2+2ax+b2=0 .
(1)若a,b都是从集合{1,2,3,4}中任取的数字,求方程有实根的概率;
(2)若a是从区间中任取的数字,b是从区间中任取的数字,求方程有实根的概率.
22、(本小题满分12分)已知椭圆C:![]()
![]() +
+![]()
![]() =1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),
=1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),
△AF1F2为正三角形且周长为6.
(1)求椭圆C的标准方程及离心率;
(2)O为坐标原点,P是直线F1A上的一个动点,求|PF2|+|PO|的最小值,并求出此时点P的坐标.
2016-2017学年第一学期高二第三次调研考试数学答案
一、选择题
1、C
2、D
【解析】![]() ,故
,故![]() ,所以方程是
,所以方程是![]()
3、C
【解析】根据样本容量的定义可知,某校有40个班,每班50人,每班派3人参加“学代会”,在这个问题中样本容量是120,选C
4.A
【解析】
试题分析:因为命题P:x>0,y>0,那么对于两个正数x,y来说,他们的积必定为正数,因此可知条件可以推出结论,但是当xy>0时,可能x,y都是负数,不一定推出条件,因此可知结论不能推出条件,因此得到p是q的充分而不必要条件,选A.
5.D
【解析】该双曲线的标准方程为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 。
。
6.C
【解析】∵4(sinB-sinA)=3sinC,∴由正弦定理得4|AC|-4|BC|=3|AB|,
即|CA|-|CB|=![]() ×8=6.∴C点的轨迹是以A、B为焦点的双曲线的上支.
×8=6.∴C点的轨迹是以A、B为焦点的双曲线的上支.
7.B
【解析】由题意![]() ,所以
,所以![]() ,由双曲线的定义,有
,由双曲线的定义,有![]() ,所以
,所以![]() ,∴
,∴![]() ,故选B.
,故选B.
8.C
【解析】函数y=|x-2|+|x|的值域为的频数是13,(20,30]的频数是24,(30,40]的频数是15,(40,50]的频数是16,∴(10,50)上的频数是13+24+15+16=68,∴样本数据落在(10,50)上的频率为68:100=0.68,
12.D
【解析】由函数![]() 在
在![]() 上为减函数可得:对称轴
上为减函数可得:对称轴![]() ,即
,即![]() .
.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
基本事件的个数为36,而满足“![]() ”的基本事件有
”的基本事件有![]() ,
,![]() ,
,![]()
![]() …共有30个,所以概率为
…共有30个,所以概率为![]() .
.
二、填空题
13、5√2 14、![]()
15、![]()
【解析】由题意知![]() ,
,![]()
![]() 从而数据
从而数据![]() ,
,![]() 这7个数据的平均数为
这7个数据的平均数为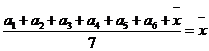 ,故这7个数据的方差为
,故这7个数据的方差为![]()
16.![]()
【解析】
![]() 则
则![]() 的面积
的面积![]() .
.
三、简答题
17.抛物线方程为![]() 或
或![]()
【解析】设方程为![]() 或
或![]() ,
,
将![]() 代入得
代入得![]() .
.
故所求抛物线方程![]() 为
为![]() 或
或![]() .
.
18.(1) b=-1 (2) (x-2)2+(y-1)2=4
【解析】
解:(1)由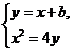
![]() 得x2-4x-4b=0.(*)
得x2-4x-4b=0.(*)
因为直线l与抛物线C相切,
所以Δ=(-4)2-4×(-4b)=0,
解得b=-1.
(2)由(1)可知b=-1,故方程(*)即为x2-4x+4=0,
解得x=2.将其代入x2=4y,得y=1.故点A(2,1).
因为圆A与抛物线C的准线相切,
所以圆A的半径r等于圆心A到抛物线的准线y=-1的距离,
即r=|1-(-1)|=2,
所以圆A的方程为(x-2)2+(y-1)2=4.
19.解:(I)设C:![]() 设
设![]()
由条件知![]() ,
,![]() ,∴
,∴![]() …………3分
…………3分
故C的方程为: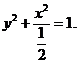 …………5分
…………5分
(II)设![]() 与椭圆C交点为A(
与椭圆C交点为A(![]() ),B(
),B(![]() )
)
由![]() 得
得![]()
得(k2+2)x2+2kmx+(m2-1)=0
![]() (*)
(*)
![]() …………8分
…………8分
∵![]() ∴
∴![]() ∴
∴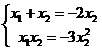
消去![]() ,得
,得![]() ,∴
,∴![]()
整理得![]()
![]() …………10分
…………10分
![]() 时,上式不成立;
时,上式不成立; ![]() 时,
时,![]() ,
,
由(*)式得![]()
因![]() ∴
∴![]() ,∴
,∴![]() 或
或![]()
即所求![]() 的取值范围为
的取值范围为![]() …………13分
…………13分
20.(1)记AC与BD的交点为O,连接OE,
∵O、M分别是AC、EF的中点,ACEF是矩形,
∴四边形AOEM是平行四边形,∴AM∥OE
∵OE⊂平面BDE,AM⊄平面BDE,∴AM∥平面BDE
(2)在平面AFD中过A作AS⊥DF于S,连接BS,
∵AB⊥AF,AB⊥AD,AD∩AF=A,∴AB⊥平面ADF,
∴AS是BS在平面ADF上的射影,
由三垂线定理得BS⊥DF
∴∠BSA是二面角A﹣DF﹣B的平面角
在Rt△ASB中,AS=![]() =
=![]() ,AB=
,AB=![]() ,
,
∴tan∠ASB=![]() ,∠ASB=60°,∴二面角A﹣DF﹣B的大小为60°;
,∠ASB=60°,∴二面角A﹣DF﹣B的大小为60°;
(3)如图设P(t,t,0)(0≤t≤![]() ),
),
则![]() =(
=(![]() ﹣t,
﹣t,![]() ﹣t,1),
﹣t,1),![]() =(
=(![]() ,0,0)
,0,0)
又∵![]() ,
,![]() 夹角为60°,∴
夹角为60°,∴![]() ,
,
解之得t=![]() 或t=
或t=![]() (舍去),
(舍去),
故点P为AC的中点时满足题意.
21.(1)![]() (2)
(2)![]()
【解析】(1)设事件A=“方程有实根”,记![]() 为取到的一种组合,则所有的情况有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4) ……2分
为取到的一种组合,则所有的情况有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4) ……2分
一共16种且每种情况被取到的可能性相同, ……3分
∵关于![]() 的一元二次方程
的一元二次方程![]() 有实根,
有实根,
∴ ![]() ……4分
……4分
∴事件A包含的基本事件有:
(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),(4,1),
(4,2),(4,3),(4,4)共10种, ……5分
![]() , ∴方程有实根的概率是
, ∴方程有实根的概率是![]() . ……6分
. ……6分
(2)设事件B=“方程有实根”,记![]() 为取到的一种组合,
为取到的一种组合,
∵![]() 是从区间中任取的数字,
是从区间中任取的数字,![]() 是从区间中任取的数字,
是从区间中任取的数字,
 ∴点
∴点![]() 所在区域是长为4,宽为3的矩形区域,如图所示:
所在区域是长为4,宽为3的矩形区域,如图所示:
……9分
又满足:![]() 的点的区域是如图所示的阴影部分,
的点的区域是如图所示的阴影部分,
∴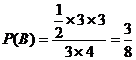 ,∴方程有实根的概率是
,∴方程有实根的概率是![]() . …12分
. …12分
22.(1) ![]()
![]() +
+![]()
![]() =1 e=
=1 e=![]() (2)
(2) ![]() (
(![]() ,
,![]()
![]() )
)
【解析】
解:(1)由题设得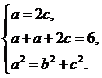
![]() 解得a=2,b=
解得a=2,b=![]()
![]() ,c=1.
,c=1.
故C的方程为![]()
![]() +
+![]()
![]() =1,离心率e=
=1,离心率e=![]()
![]() .
.
(2)直线F1A的方程为y=![]()
![]() (x+1),
(x+1),
设点O关于直线F1A对称的点为M(x0,y0),
则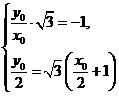
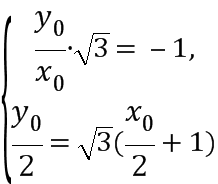 ⇒
⇒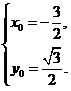
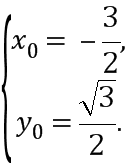
所以点M的坐标为(-![]()
![]() ,
,![]()
![]() ).
).
∵|PO|=|PM|,|PF2|+|PO|=|PF2|+|PM|≥|MF2|,
|PF2|+|PO|的最小值为
|MF2|=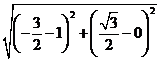
![]() =
=![]()
![]() .
.
直线MF2的方程为y=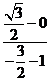
![]() (x-1),即y=-
(x-1),即y=-![]()
![]() (x-1).
(x-1).
由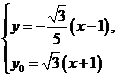
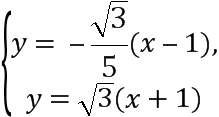 ⇒
⇒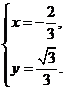
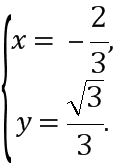
所以此时点P的坐标为(![]() ,
,![]()
![]() ).
).