类型一  求展开式中指定的项或某一项的系数或二项式系数

使用情景：求展开式中指定的项或某一项的系数或二项式系数

解题模板：第一步  首先求出二项展开式的通项；

第二步   根据已知求出展开式中指定的项或某一项的系数或二项式系数；

第三步   得出结论.

例1. 展开式中第3项的二项式系数为（      ）

A．6      B．-6        C．24       D．-24

【答案】A

【解析】

 

(2)已知展开式的某项，求特定项的系数.可由某项得出参数项，再由通项写出第r＋1项，由特定项得出r值，最后求出其参数.

【变式演练1】二项式展开式中，项的系数为           ．

【答案】

【解析】

试题分析：，所以由得系数为

考点：二项式定理

【方法点睛】求二项展开式有关问题的常见类型及解题策略

(1)求展开式中的特定项.可依据条件写出第r＋1项，再由特定项的特点求出r值即可.

(2)已知展开式的某项，求特定项的系数.可由某项得出参数项，再由通项写出第r＋1项，由特定项得出r值，最后求出其参数.

【变式演练2】的展开式中项的系数为20，则实数 ．

【答案】

【解析】

试题分析：二项式展开式的通项为，令，解得，故展开式中项的系数为，解得.

考点：二项式定理．

【变式演练3】求的展开式中的系数.

【答案】．

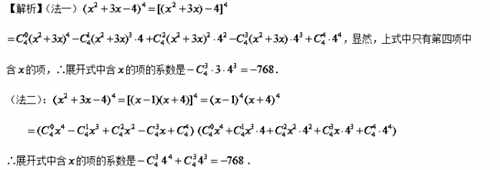考点：二项式定理．

类型二  二项式系数的性质与各项系数和

使用情景：二项式系数的性质与各项系数和

解题模板：第一步   观察题意特征，合理地使用赋值法；

第二步   区别二项式系数与展开式中项的系数，灵活利用二项式系数的性质；

第三步   得出结论.

例2 (1)设(1＋x)ⁿ＝a₀＋a₁x＋a₂x²＋…＋a_nxⁿ，若a₁＋a₂＋…＋a_n＝63，则展开式中系数****的项是(　　)

A．15x²  B．20x³  C．21x³  D．35x³

(2)若x(1)的展开式中第3项与第7项的二项式系数相等，则该展开式中x2(1)的系数为________．

【答案】(1)B；(2)56.

【解析】

点评：(1)第(1)小题求解的关键在于赋值，求出a₀与n的值；第(2)小题在求解过程中，常因把n的等量关系表示为Cn(3)＝Cn(7)，而求错n的值．(2)求解这类问题要注意：①区别二项式系数与展开式中项的系数，灵活利用二项式系数的性质；②根据题目特征，恰当赋值代换，常见的赋值方法是使得字母因式的值或目标式的值为1，－1. 

【变式演练4】在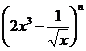的展开式中，各二项式系数的和为128，则常数项是__________．

【答案】14.

【解析】

试题分析：因为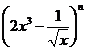的展开式中，各二项式系数的和为128，所以，即，所以

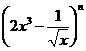的展开式的通项为，令，则

，即常数项是，故应填14.

考点：1、二项式定理的应用.