类型三  二项式定理的应用

使用情景：使用二项式定理处理整除问题

解题模板：第一步   通常把底数写成除数(或与余数密切相关联的数)与某数的和或差的形式；

第二步   再用二项式定理展开，但要注意两点：一是余数的范围，a＝cr＋b，其中余数b∈0，

r)，r是除数，切记余数不能为负，二是二项式定理的逆用．；

第三步   得出结论.

例3 .设a∈Z，且0≤a<13，若51^{2 012}＋a能被13整除，则a＝(　　)

A．0             B．1          C．11         D．12

【答案】D.

【解析】

点评：在使用二项式定理展开，但要注意两点：一是余数的范围，a＝cr＋b，其中余数b∈0，r)，r是除数，切记余数不能为负，二是二项式定理的逆用．

【变式演练5】S＝C27(1)＋C27(2)＋…＋C27(27)除以9的余数为________．

【答案】7.

【解析】

考点：二项式定理．

【高考再现】

1. 【2016年高考四川理数】设i为虚数单位，则的展开式中含x⁴的项为

（A）－15x⁴     （B）15x⁴     （C）－20i x⁴     （D）20i x⁴

【答案】A

【解析】

试题分析：二项式展开的通项，令，得，则展开式中含的项为，故选A.

考点：二项展开式，复数的运算.

【名师点睛】本题考查二项式定理及复数的运算，复数的概念及运算也是高考的热点，几乎是每年必考内容，属于容易题.一般来说，掌握复数的基本概念及四则运算即可．二项式的展开式可以改为，则其通项为，即含的项为．

2. 【2016年高考北京理数】在的展开式中，的系数为__________________.（用数字作答）

【答案】60.

【解析】

试题分析：根据二项展开的通项公式可知，的系数为，故填：.

考点：二项式定理.

【名师点睛】1.所谓二项展开式的特定项，是指展开式中的某一项，如第项、常数项、有理项、字母指数为某些特殊值的项.求解时，先****写出通项，再把系数与字母分离出来(注意符号)，根据题目中所指定的字母的指数所具有的特征，列出方程或不等式来求解即可；2、求有理项时要注意运用整除的性质，同时应注意结合的范围分析.

3. 【2016高考新课标1卷】的展开式中,x³的系数是         .（用数字填写答案）

【答案】

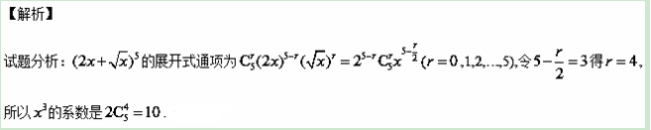考点:二项式定理

4. 【2016高考天津理数】的展开式中x²的系数为__________.(用数字作答)

【答案】

【解析】

试题分析：展开式通项为，令，，所以的．故答案为． 

考点：二项式定理

5. 【2016高考山东理数】若（ax²+）⁵的展开式中x⁵的系数是—80，则实数a=_______.

【答案】-2

【解析】

试题分析：因为，所以由，因此

考点：二项式定理

【名师点睛】本题是二项式定理问题中的常见题型，二项展开式的通项公式，往往是考试的重点.本题难度不大，易于得分.能较好的考查考生的基本运算能力等.

6.【2015高考天津，理12】在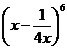 的展开式中，的系数为        .

【答案】

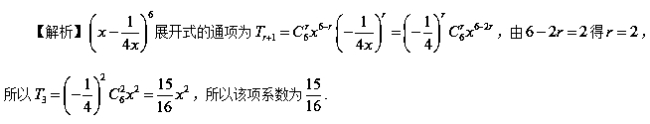7. 【2016高考江苏卷】（本小题满分10分）

（1）求 的值；

（2）设m，nN^*，n≥m，求证： 

（m+1）+（m+2）+（m+3）+…+n+（n+1）=（m+1）.

【答案】（1）0（2）详见解析

【解析】

试题分析：（1）根据组合数公式化简求值（2）设置（1）目的指向应用组合数性质解决问题，而组合数性质不仅有课本上的  ，而且可由（1）归纳出的  ；单纯从命题角度看，可视为关于n的等式，可结合数学归纳法求证；从求和角度看，左边式子可看做展开式中含项的系数，再利用错位相减求和得含项的系数 ，从而达到化简求证的目的

试题解析：解：（1）

考点：组合数及其性质

【名师点睛】本题从性质上考查组合数性质，从方法上考查利用数学归纳法解决与自然数有关命题，从思想上考查运用算两次解决二项式有关模型. 组合数性质不仅有课本上介绍的、，更有，现在又有，这些性质不需记忆，但需会推导，更需会应用.

【反馈练习】

1．【山东省肥城市2017届高三上学期升级统测，12】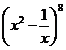 的展开式中的的系数是         ．

【答案】

【解析】

试题分析：，由得，系数是

考点：二项式定理

【方法点睛】求二项展开式有关问题的常见类型及解题策略

(1)求展开式中的特定项.可依据条件写出第r＋1项，再由特定项的特点求出r值即可.

(2)已知展开式的某项，求特定项的系数.可由某项得出参数项，再由通项写出第r＋1项，由特定项得出r值，最后求出其参数.

2.【河北省衡水中学2017届高三摸底联考，13】的展开式中项的系数为         ．

【答案】

【解析】

试题分析：的展开式中项的系数为,故填.

考点：二项式定理.

3.【广东海珠区2017届上学期高三综合测试（一），13】二项式的展开式中常数项为          .

【答案】  

【解析】

考点：二项展开式的通项公式.

4．【河南百校联考2017届高三9月质检，14】若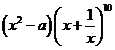的展开式中的系数为30，则____________．

【答案】10

【解析】

试题分析：由题意得，所以

考点：二项式定理，定积分

【方法点睛】求二项展开式有关问题的常见类型及解题策略

(1)求展开式中的特定项.可依据条件写出第r＋1项，再由特定项的特点求出r值即可.

(2)已知展开式的某项，求特定项的系数.可由某项得出参数项，再由通项写出第r＋1项，由特定项得出r值，最后求出其参数.