6．【云南省、四川省、贵州省2017届高三上学期百校大联考数学，15】 的展开式中的系数为______________.

【答案】30

【解析】

试题分析：因为的通项公式为，所以的展开式中含的奇数次方的通项为，令，解得.从而所求的系数为.

考点：二项式定理. 

【思路点睛】本题考查二项式定理，二项展开式的通项公式，求展开式中某项的系数，根据的展开式的含的项由两类构成，然后求出各类的含的项，再将各个项加起来，即可得到所求的项的系数．

7．【湖北省黄石市2017届高三年级九月份调研，16】将三项式展开，当时，得到如下左图所示的展开式，右图所示的广义杨辉三角形：

                                               第0行          1

                                        第1行        1 1 1

                            第2行       1 2 3 2 1

                  第3行      1 3 6 7 6 3 1

   第4行  1 4 10 16 19 16 10 4 1

……

观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法：第0行为1，以下各行每个数是它头上与左右两肩上3数（不足3数的，缺少的数计为0）之和，第行共有个数．若在的展开式中，项的系数为75，则实数的值为___________．

【答案】2

【解析】

考点：新定义

8．【江西省新余市2016届高三第二次模拟考试数学（理）试题】展开式中除常数项外的其余项的系数之和为        .

【答案】

【解析】

试题分析：令,得各项系数和为,展开的通项,令,所以,除常数项外的其余项的系数之和为.

考点：二项式定理.

9．【山西省临汾一中、忻州一中、长治二中等五校2017届高三上学期第二次联考数学（理）试题】已知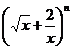的展开式中的第四项为常数项，则        .

【答案】

【解析】

试题分析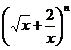：的展开式通项为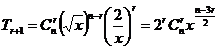,由展开式中第四项为常数项,即时,,,故填.

考点：二项式定理.

10．【广西梧州市2017届高三上学期摸底联考数学（理）试题】在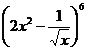的展开式中，含的项的系数是（   ）

A．60                        B．160                       C．180                      D．240

【答案】D

【解析】

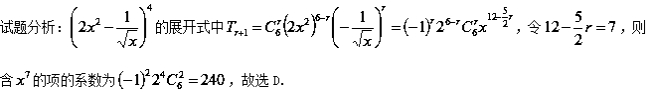考点：二项式定理.

11．【2016-2017学年江西崇仁县二中高二上期中数学（理）试卷】若(2x－3)⁵＝a₀＋a₁x＋a₂x²＋a₃x³＋a₄x⁴＋a₅x⁵，则a₁＋2a₂＋3a₃＋4a₄＋5a₅＝________．

【答案】10

【解析】原等式两边求导得5(2x－3)⁴·(2x－3)′＝a₁＋2a₂x＋3a₃x²＋4a₄x³＋5a₅x⁴，令上式中x＝1，得a₁＋2a₂＋3a₃＋4a₄＋5a₅＝10.

考点：二项式定理．

12．【2017届贵州遵义市高三上期中数学（文）试卷】求证：1＋2＋2²＋…＋2^5n－1(n∈N^*)能被31整除．

【答案】详解见解析.

考点：二项式定理．

13. 【2016-2017学年河北定州中学高二周练10.9数学试卷】已知 的展开式中含项的系数为，求展开式中含项的系数最小值

【答案】详解见解析.

考点：二项式定理．