若不等式组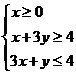所表示的平面区域被直线分为面积相等的两部分，则k的值是

A．   B．

C．   D．

【答案】A

【解析】不等式组表示的平面区域如图所示．

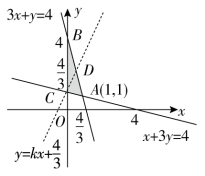
由于直线过定点.因此只有直线过AB中点时，直线能平分平面区域．因为A(1,1)，B(0,4)，所以AB中点.当过点时，即，所以.

【考点定位】二元一次不等式(组)表示的平面区域.

【名师点评】一般情况下,对于不是标准形式的二元一次不等式,要作出它所表示的平面区域,可以先把它化成标准形式,再作图.

设x，y满足约束条件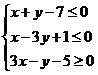，则z=2x−y的****值为

A．10   B．8

C．3   D．2

【答案】B

【解析】作出可行域如图中阴影部分所示，由z=2x−y得y=2x−z，作出直线y=2x，平移使之经过可行域，观察可知，当直线经过点A(5,2)时，对应的z值****，故z_max=2×5−2=8.故选B.

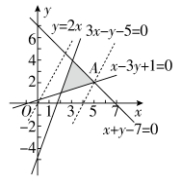
【考点定位】由线性目标函数求最值.

【名师点睛】本题解题的关键是正确画出不等式组表示的可行域，从而可得解.对于此类问题，也可将各个顶点直接求出，代入目标函数，再比较大小即可.

 设x，y满足约束条件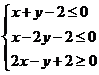，若z=y−ax取得****值的最优解不****，则实数a的值为

A．或−1   B．2或

C．2或1   D．2或−1

【答案】D

【解析】解法一：由题中条件画出可行域如图中阴影部分所示，可知A(0,2)，B(2,0)，C(−2，−2)，则z_A=2，z_B=−2a，z_C=2a−2，要使目标函数取得****值的最优解不****，只要z_A=z_B>z_C或z_A=z_C>z_B或z_B=z_C>z_A，解得a=−1或a=2.

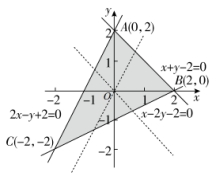
解法二：目标函数z=y−ax可化为y=ax＋z，令l₀∶y=ax，平移l₀，则当l₀∥AB或l₀∥AC时符合题意，故a=−1或a=2.

【考点定位】由线性目标函数的最值求参数

【名师点睛】最优解不****或者有无穷多个，往往是指目标函数所对应的直线与约束条件中二元一次不等式所表示的边界直线重合.

已知变量x、y满足.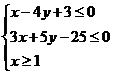

（1）设，求z的最小值；

（2）设，求z的取值范围；

（3）设，求z的取值范围．

【答案】（1）；（2）；（3）.

【解析】（1）由约束条件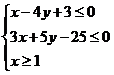作出可行域如图所示．

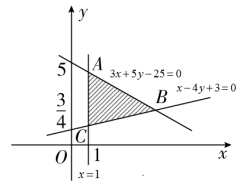
由，解得.

由，　解得．

由，解得．

∵.

∴z的值即是可行域中的点与原点O连线的斜率．观察图形可知z_min=k_OB=.

（2）的几何意义是可行域上的点到原点O的距离的平方．结合图形可知，可行域上的点到原点的距离中，d_min=|OC|=，d_max=|OB|=.

∴2≤ z ≤29.

（3）的几何意义是可行域上的点到点(−3,2)的距离的平方．结合图形可知，可行域上的点到(−3,2)的距离中，d_min=1−(−3)=4，d_max=.

∴16≤ z ≤64.

【考点定位】非线性目标函数的最值.

【名师点睛】（1）斜率问题是线性规划延伸变化的一类重要问题，其本质仍然是二元函数的最值问题，不过是用模型形态呈现的.因此有必要总结常见模型或其变形形式.（2）距离问题常涉及点到直线的距离和两点间的距离，熟悉这些模型有助于更好地求解非线性目标函数的最值.

某旅行社租用A，B两种型号的客车安排900名客人旅行，A，B两种车辆的载客量分别为36人和60人，租金分别为1600元/辆和2400元/辆，旅行社要求租车总数不超过21辆，且B型车不多于A型车7辆，则租金最少为

A．31200元   B．36000元

C．36800元   D．38400元

【答案】C

【解析】设租A型车x辆，B型车y辆，租金为z，则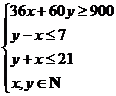，即.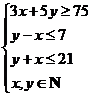

画出可行域(图中阴影区域中的整数点).

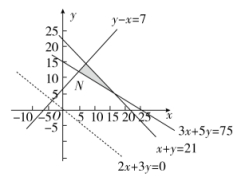
则目标函数z=1600x＋2400y在点N(5,12)处取得最小值36800元．

【考点定位】线性规划的实际应用.

【名师点睛】对于有实际背景的线性规划问题,可行域通常是位于第一象限内的一个凸多边形区域,此时最优解一般在这个凸多边形的顶点处取得.

1．若实数x、y满足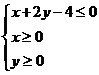，则的取值范围为

A． B． 

C． D．

2．已知实数x，y满足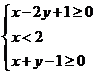，则z=2x−2y−1的取值范围是

A．             B．0,5]            C．         D．

3．已知点P(x，y)的坐标满足条件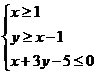，那么点P到直线3x−4y−13=0的距离的最小值为

A．                B．2              C．             D．1

4．在坐标平面内，不等式组所表示的平面区域的面积为

A．               B．            C．          D．2

5．已知实数x，y满足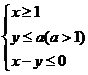，若z=x＋y的****值为4，则实数a的值为

A．2                   B．3             C．4               D．

6．某公司生产甲、乙两种桶装产品．已知生产甲产品1桶需耗A原料1千克、B原料2千克；生产乙产品1桶需耗A原料2千克、B原料1千克．每桶甲产品的利润是300元，每桶乙产品的利润是400元．公司在生产这两种产品的计划中，要求每天消耗A、B原料都不超过12千克．通过合理安排生产计划，从每天生产的甲、乙两种产品中，公司共可获得的****利润是

A．1800元             B．2400元        C．2800元         D．3100元

7．若实数x，y满足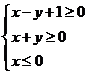，则z=3^x, ^＋2y的值域是___________.

8．若x，y满足约束条件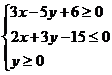，当且仅当x=y=3时，z=ax＋y取得****值，则实数a的取值范围是___________．

1．B 【解析】作出不等式组对应的平面区域，如图．因为，所以z的几何意义是区域内过任意一点(x，y)与点P(1，−2)的直线的斜率．由题意知C(4,0)，所以，所以的取值范围为或z ≤−2，即.故选B.

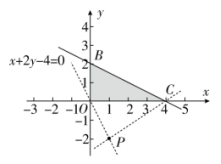
2．D 【解析】画出不等式组所表示的区域如图中阴影部分所示，作直线l：2x−2y−1=0，平移l可知当l过点C和B(2，−1)时，z分别取最小值和****值.2×−2×−1≤ z <2×2−2×(−1)−1，即z的取值范围是.

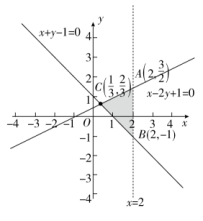
 3．B 【解析】在坐标平面内画出题中的不等式组表示的平面区域及直线3x−4y−13=0，由图可知，在该平面区域内所有的点中，到直线3x−4y−13=0的距离最近的点是A(1,0)．又点A(1,0)到直线3x−4y−13=0的距离等于，即点P到直线3x−4y−13=0的距离的最小值为2，选B.

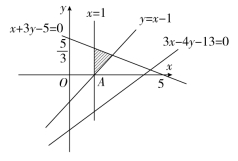
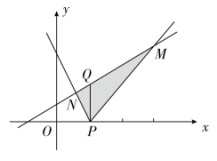
4．B 【解析】不等式组⇔不等式组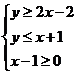或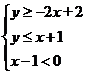，画出两不等式组所表示的平面区域．如图，M(3,4)，，P(1,0)，Q(1,2)，所以不等式组所表示的平面区域的面积为×2×2＋×2×=.故选B.

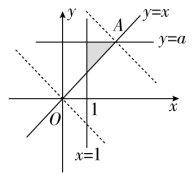
5．A 【解析】由约束条件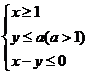作出可行域为如图所示的阴影部分，当z=x+y过y=x和y=a的交点A(a，a)时，z取得****值，即z_max=a+a=4，所以a=2.故选A.

6．C 【解析】设每天生产甲种产品x桶，乙种产品y桶，则根据题意得x、y的约束条件为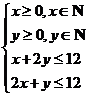，设获利z元，则z=300x＋400y.画出可行域如图．

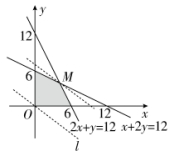
画直线l：300x＋400y=0，即3x＋4y=0.

平移直线l，从图中可知，当直线过点M时，目标函数取得****值．

由，解得，即M的坐标为(4,4)，∴z_max=300×4＋400×4=2800(元)．故选C.

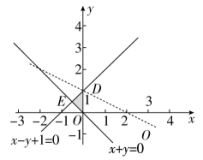
7．1,9] 【解析】令t=x+2y，则y=−x+，作出可行域，平移直线y=−x，由图象知当直线经过O点时，t最小，当经过点D(0,1)时，t****，所以0≤ t ≤2，所以1=3⁰≤ z ≤3²=9，即z=3^x＋2y的值域是1,9]．

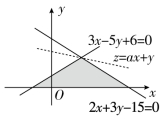
8．【解析】直线3x−5y＋6=0和直线2x＋3y−15=0的斜率分别为.作出可行域如图所示，当且仅当直线z=ax＋y经过点(3,3)时，z取得****值，则直线z=ax＋y的斜率−a满足，解得.