1.　命题p：x∈{x|x²＋2x－3>0}，命题q：x∈{x|3－x(1)>1}，若p∧q为真，求 x的取值范围.

【解析】当p为真时得：x>1或x<－3；当q为真时得：2<x<3，因为p∧q为真，则p真且q真，即求{x|x>1或x<－3}与{x|2<x<3}的交集为(2,3).

2.已知命题p：“∀x∈1,2]，x²－a≥0”，命题q：“∃x₀∈R，＋2ax₀＋2－a＝0”.若命题“∧q”是真命题，求实数a的取值范围.

3.若“∀x∈4(π)，m≤tanx＋1”为真命题，求实数m的****值.

【解析】令f(x)＝tanx＋1，则函数f(x)在4(π)上为增函数，故f(x)的最小值为f4(π)＝0，

∵∀x∈4(π)，m≤tanx＋1，

故m≤(tanx＋1)_min，

∴m≤0，故实数m的****值为0.

4.如图（1）所示,在直角梯形ABCD中, BC∥AP, ABBC,CDAP,

AD=DC=PD=2.又 E、F、G 分别为线段PC、PD、BC的中点,现将△PDC折起,使平面

PDC⊥平面ABCD（图（2））．

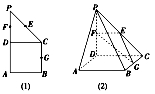
（1）求证：平面EFG∥平面PAB；

（2）求三棱锥C-EFG的体积．

【解析】（1）∵E、F分别是PC，PD的中点，

∴EF∥CD又CD∥AB． ∴ EF∥AB． 

∵EF平面PAB，AB平面PAB， 

∴EF∥平面PAB．同理，EG∥平面PAB，

∵，EF平面EFG，EG 平面EFG

∴平面EFG∥平面PAB．               

（2）V_C－EFG＝V_G－CEF＝S_△CEF·GC＝×（×1×1）×1＝．

5. 已知p：∃x₀∈R，mx0(2)＋2≤0，q：∀x∈R，x²－2mx＋1>0，若p∨q为假命题，求实数m的取值范围.

6.椭圆4(x2)＋3(y2)＝1的离心率为e，点(1，e)是圆x²＋y²－4x－4y＋4＝0的一条弦的中点，求此弦所在直线的方程

【解析】依题意得e＝2(1)，圆心坐标为(2，2)，圆心(2，2)与点(1，2(1))的连线的斜率为2()＝2(3)，

所求直线的斜率为－3(2)，所以所求直线方程是y－2(1)＝－3(2)(x－1)．即4x＋6y－7＝0.

7.已知椭圆C₁：4(x2)＋b2(y2)＝1(0<b<2)的离心率为2(3)，抛物线C₂：x²＝2py(p>0)的焦点是椭圆的顶点．

(1)求抛物线C₂的方程．

(2)过点M(－1，0)的直线l与抛物线C₂交于E，F两点，过E，F作抛物线C₂的切线l₁，l₂，当l₁⊥l₂时，求直线l的方程．

【解析】(1)∵椭圆C₁的长半轴长a＝2，半焦距c＝，由e＝a(c)＝2(4－b2)＝2(3)得b²＝1，

∴椭圆C₁的上顶点为(0，1)，

∴抛物线C₂的焦点为(0，1)，

∴抛物线C₂的方程为x²＝4y.

(2)由已知可得直线l的斜率必存在，设直线l的方程为y＝k(x＋1)， E(x₁，y₁)，F(x₂，y₂)．由x²＝4y得y＝4(1)x²，∴y′＝2(1)x.∴切线l₁，l₂的斜率分别为2(1)x₁，2(1)x₂.

当l₁⊥l₂时，2(1)x₁·2(1)x₂＝－1，即x₁x₂＝－4.

由x2＝4y(y＝k（x＋1）)得x²－4kx－4k＝0，

∴Δ＝(4k)²－4×(－4k)>0，解得k<－1或k>0.①

且x₁x₂＝－4k＝－4，得k＝1，满足①式．

∴直线l的方程为x－y＋1＝0.

8.  已知双曲线的方程为2x²－y²＝2.

(1)求以A(2，1)为中点的双曲线的弦所在直线的方程；

(2)过点B(1，1)能否作直线l，使l与所给双曲线交于Q₁，Q₂两点，且点B是弦Q₁Q₂的中点？如果l存在，求出它的方程；如果不存在，说明理由．

9.已知中心在原点，焦点在轴上的椭圆C的离心率为，且经过点，过点P（2，1）的直线与椭圆C在第一象限相切于点M ．

（1）求椭圆C的方程；

（2）求直线的方程以及点M的坐标；

（3） 是否存过点P的直线与椭圆C相交于不同的两点A、B，满足？若存在，求出直线l₁的方程；若不存在，请说明理由．

因为直线与椭圆相切，所以

整理，得 解得

所以直线l方程为

将代入①式，可以解得M点横坐标为1，故切点M坐标为……8分

（Ⅲ）若存在直线l₁满足条件，的方程为，代入椭圆C的方程得

因为直线l₁与椭圆C相交于不同的两点A，B，设A，B两点的坐标分别为

所以

所以．

又，

因为即，

所以．

即

所以，解得  因为A，B为不同的两点，所以．

于是存在直线₁满足条件，其方程为

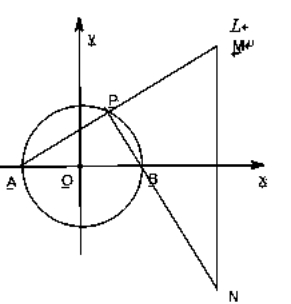
10.已知圆的直径AB=4，定直线到圆心的距离为4，且直线⊥直线AB. 点P是圆O上异于A、B的任意一点，直线PA、PB分别交与M、N点. 如图，以AB为轴，圆心O为原点建立平面直角坐标系.

（Ⅰ）若∠PAB=30°，求以MN为直径的圆方程；

（Ⅱ）当点P变化时，求证：以MN为直径的圆必过圆O内的一定点.

 ∴，MN=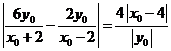

MN的中点坐标为以MN为直径的圆截x轴的线段长度为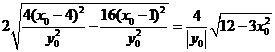

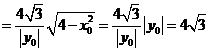为定值∴⊙必过⊙O 内定点. ----12分

11．如图，在四面体中，截面是平行四边形，

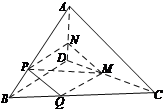
(1)求证：截面

(2)若截面是正方形，求异面直线与所成的角.

所以异面直线与所成的角是.

【方法点睛】本题考查了线面平行，以及异面直线所成角的问题，属于基础题型，重点说说空间角的问题，（1）异面直线所成角，几何法：通过平移转化为相交直线所成角，然后在三角形内解三角形，向量法：转化为异面直线的方向向量所成角，通过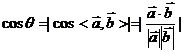求解；（2）线面角，几何法：线面角就是线与其在平面内的射影所成角，一般可通过直线外一点向平面内引垂线，连接垂足与斜足的线就是线在平面内的射影，向量法：先求法向量，求解；（3）面面角，几何法：①定义法，②垂面法，③三垂线法或其逆定理法，向量法：先求两个平面内的法向量，那么或.