12.如图,一个几何体的三视图△![]() 是边长为的等边三角形,
是边长为的等边三角形,
(Ⅰ)画出直观图;
(Ⅱ)求这个几何体的体积
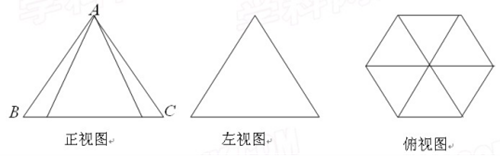
【解析】(Ⅰ)如图;
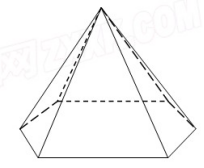
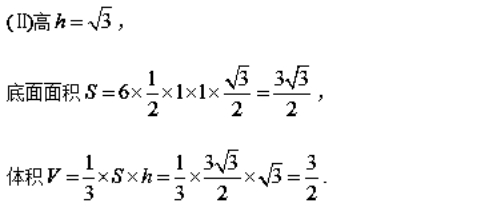
13.一个正四棱台的斜高为12,侧棱长为13,侧面积为720,求它的体积.
【解析】设该棱台的上、下底面边长分别为和,高为,斜高为![]() ,侧棱长为,
,侧棱长为,

![]() .
.
14.已知点![]() ,
,![]() ,求线段
,求线段![]() 的垂直平分线的方程.
的垂直平分线的方程.
【解析】已知两点![]() ,
,![]() ,则线段
,则线段![]() 的中点
的中点![]() 坐标是
坐标是![]() .
.
因为直线![]() 的斜率为
的斜率为![]() ,所以,线段
,所以,线段![]() 的垂直平分线的斜率是
的垂直平分线的斜率是![]() .
.
因此,线段![]() 的垂直平分线的方程是
的垂直平分线的方程是![]() .即
.即![]() .
.
15.已知圆![]() 内有一点
内有一点![]() ,过点
,过点![]() 作直线交圆
作直线交圆![]() 于
于![]() 两点.
两点.
(Ⅰ)当经过圆心![]() 时,求直线的方程;
时,求直线的方程;
(Ⅱ)当直线的倾斜角为![]() 时,求弦
时,求弦![]() 的长.
的长.
【解析】(Ⅰ)已知圆![]() 的圆心为
的圆心为![]() ,
,
因直线过点![]() ,所以直线的斜率为,
,所以直线的斜率为,
直线的方程为![]() ,即
,即![]()
(Ⅱ)当直线的倾斜角为![]() 时,斜率为,直线的方程为
时,斜率为,直线的方程为![]() ,
,
即![]()
圆心![]() 到直线的距离为
到直线的距离为![]() ,
,
又圆的半径为,弦![]() 的长为
的长为![]() .
.
16.如图,在多面体![]() 中,四边形
中,四边形![]() 为正方形,
为正方形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
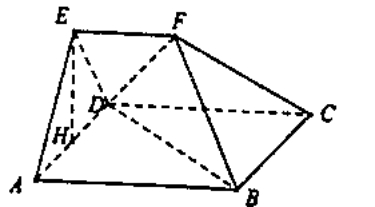
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

设点![]() ,于是有
,于是有![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,则
,则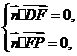 即
即![]()
令![]() ,得
,得![]() ,
,![]() ,所以
,所以![]() .
.
平面![]() 的法向量
的法向量![]() ,所以
,所以![]() ,
,
即,所以![]() .
.
所以点![]() 的坐标为
的坐标为![]() ,与点
,与点![]() 的坐标相同,所以
的坐标相同,所以![]() .
.
17.抛物线顶点在原点,焦点在x轴上,且过点(4,4),焦点为F.
(1)求抛物线的焦点坐标和标准方程:
(2)P是抛物线上一动点,M是PF的中点,求M的轨迹方程.

18.已知椭圆![]() 过点A(a,0),B(0,b)的直线倾斜角为
过点A(a,0),B(0,b)的直线倾斜角为![]() ,原点到该直线的距离为
,原点到该直线的距离为![]() .
.
(1)求椭圆的方程;
(2)斜率小于零的直线过点D(1,0)与椭圆交于M,N两点,若![]() 求直线MN的方程;
求直线MN的方程;
【解析】:(Ⅰ)由![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,
所以椭圆方程是:![]() ……………………3分
……………………3分
(Ⅱ)设MN:![]() 代入
代入![]() ,得
,得![]() ,
,
![]() ,由
,由![]() ,得
,得![]() .
.
由![]() ,
,![]() ……………………6分
……………………6分
得![]() ,
,![]() ,
,![]() (舍去)
(舍去)
直线![]() 的方程为:
的方程为:![]() 即
即![]() ……………………8分
……………………8分
(Ⅲ)将![]() 代入
代入![]() ,得
,得![]() (*)
(*)
记![]() ,
,![]() ,
,![]() 为直径的圆过
为直径的圆过![]() ,则
,则![]() ,即
,即
![]() ,又
,又![]() ,
,![]() ,得
,得
![]() ………①
………①
又![]() ,代入①解得
,代入①解得![]() ……………11分
……………11分
此时(*)方程![]() ,
,![]() 存在
存在![]() ,满足题设条件.…………12分
,满足题设条件.…………12分
19.已知中心在原点,焦点在轴上的椭圆C的离心率为![]() ,且经过点
,且经过点![]() ,过点P(2,1)的直线与椭圆C在第一象限相切于点M .
,过点P(2,1)的直线与椭圆C在第一象限相切于点M .
(1)求椭圆C的方程;
(2)求直线的方程以及点M的坐标
【解析】(Ⅰ)设椭圆C的方程为![]() ,由题意得
,由题意得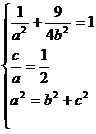

整理,得![]() 解得
解得![]()
所以直线l方程为![]()
将![]() 代入①式,可以解得M点横坐标为1,故切点M坐标为
代入①式,可以解得M点横坐标为1,故切点M坐标为![]()
20.在平面直角坐标系![]() 中,设点
中,设点![]() ,以线段
,以线段![]() 为直径的圆经过原点
为直径的圆经过原点![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线与轨迹
的直线与轨迹![]() 交于两点
交于两点![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,试判断直线
,试判断直线![]() 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论.

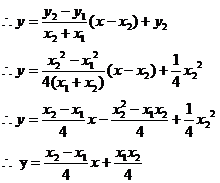
即![]()
所以,直线![]() 恒过定点
恒过定点![]() .
.